Two integers, \(a\) and \(b\), are said to be congruent modulo \(n\) if and only if their difference is divisible by \(n\). It can be written as
\(a \equiv b (mod \ n)\)
In other words, the two integers, \(a\) and \(b\), is the difference of the integer multiple of congruence modulo \(n\). That is, \(b - a = kn\) for some integer \(k\).
Here, \(n\) is called the modulus of the congruence.
Example:
\(39 \equiv 4 (mod \ 5)\). Here, \(5\) is the modulus of the congruence because \(39 - 4 = 35\) is divisible by \(5\).
Consider the following examples on how to find the congruence modulo.
Example:
1. Find \(3 (mod \ 2)\)
Solution:
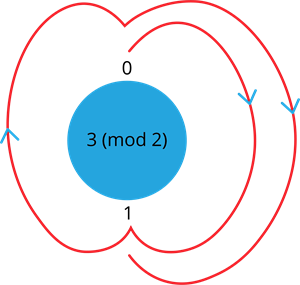
Consider the possible remainders for the number with mod \(2\) are \(0\), \(1\).
To find the remainder of the given number, start at \(0\) and go through \(3\) numbers in a clockwise direction. The \(3\) numbers would go in a cycle starting from \(0\). They are \(1\), \(0\), \(1\). Since the cycle ends at the remainder of \(1\), the answer for \(3 (mod \ 2)\) is \(1\).
Therefore, \(3 \equiv 1 (mod \ 2)\)
2. Find \(-3 (mod \ 2)\)
Solution:
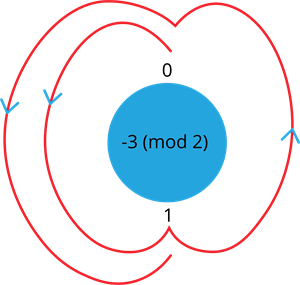
Consider the possible remainders for the number with mod \(2\) are \(0\), \(1\).
To find the remainder of the given number, start at \(0\) and go through \(3\) numbers in a anticlockwise direction(because the number has a negative sign). The \(3\) numbers would go in a cycle starting from \(0\). They are \(1\), \(0\), \(1\). Since the cycle ends at the remainder of \(1\), the answer for \(-3 (mod \ 2)\) is \(1\).
Therefore, \(-3 \equiv 1 (mod \ 2)\)