In the given figure, if \(LM||CB\) and \(LN||CD\), prove that \(\frac{AM}{AB} = \frac{AN}{AD}\).
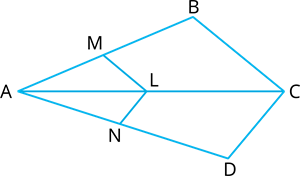
Proof:
In \(\Delta ACB\),
\(LM || CB\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{AL}{LC} =\) - - - - (1)
In \(\Delta ACD\),
\(LN || CD\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{AL}{LC} =\) - - - - (2)
From (1) and (2),
\(\frac{AM}{MB} = \)
\(\frac{MB}{AM} = \)
Simplifying we get,
\(\frac{AM}{AB} = \frac{AN}{AD}\)
Hence proved.
Answer variants:
\( \frac{AM}{MB}\)
\(\frac{AN}{ND}\)
\( \frac{AN}{ND}\)
\( \frac{ND}{AN}\)