\(ABCD\) is a trapezium in which \(AB || DC\) and its diagonals intersect each other at the point \(O\). Show that \(\frac{AO}{BO} = {CO}{DO}\).
Proof:
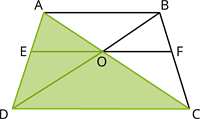
In \(\Delta ADC\),
\(EO||DC\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
So, \(\frac{AE}{DE} =\) - - - - - (1)
Similarly, in \(\Delta DBA\)
\(EO||AB\)
\(\frac{AE}{DE} =\) - - - - - (2)
From (1) and (2) we proved the result.
Answer variants:
\(\frac{BO}{DO}\)
\( \frac{AO}{CO}\)
\(\frac{BO}{CO}\)
\( \frac{AO}{DO}\)