Drag the correct answers — task. Maths CBSE Homework Assignments, Class 9.

Answer variants:

All the sides of a rhombus are equal

∠ L O M = ∠ N M O

Diagonals of a parallelogram bisect each other

Δ L O M ≅ Δ N M O

O M = O M

Δ L O M ≅ Δ M O N

∠ L O M + ∠ M O N = 180 °

∠ L O M = ∠ M O N

Using parallelogram property

Opposite sides of a parallelogram are equal

Using CPCT

O L = M N

All the sides of a parallelogram are equal

∠ L O M + ∠ N M O = 180 °

Show that the diagonals of a rhombus are perpendicular to each other.

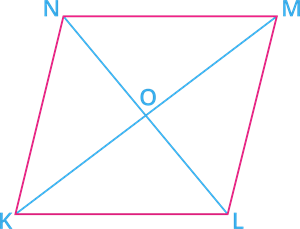
S. No.	Statement	Reason
1.	$KLMN$ is a parallelogram.	Rhombus is also a parallelogram.
2.	$O L = O N$
3.		Common side
4.	$L M = M N$
5.		$SSS$ Congruence rule
6.		CPCT
7.		Linear pair
8.	$∠ L O M = 90 °$

Hence, the diagonals of a rhombus are perpendicular to each other.

Did you find an error?

1. Drag the correct answers