In the following figure, \(KLMN\) is a rhombus. Diagonals \(KM\) and \(LN\) intersect at \(O\). \(P\) and \(Q\) are mid-points of \(OK\) and \(OL\) respectively. If \(KM\) \(=\) 14 \(cm\) and \(LN\) \(=\) 48 \(cm\), then \(PQ\) is:
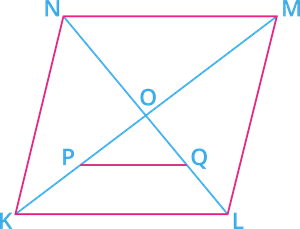
The value of \(PQ\) \(=\) \(cm\)