A linear equation in which two variables are involved in which each variable is in the first degree.
It can be written in the form \(ax + by + c = 0\) where \(a\), \(b\), \(c\) are real numbers, both \(a\) and \(b\) are not equal to zero, \(x\) and \(y\) are variables and \(c\) is a constant.
It can be written in the form \(ax + by + c = 0\) where \(a\), \(b\), \(c\) are real numbers, both \(a\) and \(b\) are not equal to zero, \(x\) and \(y\) are variables and \(c\) is a constant.
Example:
\(2x + y = 8\), \(x - y - 1 = 0\), \(y = 2x\) are examples of linear equations in two variables.
Substitution method
Let us learn how to solve the system of linear equations using the substitution method.
The steps to solve the system of linear equations using the substitution method is given by:
Step 1: From the given two equations, consider an equation. Find the value of one of the variables in terms of the other.
Step 2: Substitute the value (obtained in Step 1) in the other equation.
Step 3: Now, simplify the equation and find the value of the other unknown variable.
Step 4: Substituting the obtained value (variable in Step 3) in the equation (obtained in Step 1), we get the value of the first unknown variable.
To understand the concept clearly, let us consider an example.
Example:
Solve the simultaneous linear equations \(2x + y = 8\) and \(x + 2y = 10\) by substitution method.
Solution:
Step 1: Consider an equation and find the value of one of the variables in terms of the other.
Consider the equation \(2x + y = 8\)
Subtract \(2x\) from both the sides, we get:
\(2x + y - 2x = 8 - 2x\)
\(y = 8 - 2x\)
Step 2: Substitute the value of \(y\) in the other equation.
\(x + 2(8 - 2x) = 10\) (Substituting \(y = 8 - 2x\))
Step 3: Solve the above equation and find the value of the variable \(x\).
\(x + 16 - 4x = 10\)
\(-3x + 16 = 10\)
\(-3x = 10 - 16\)
\(-3x = -6\)
\(x = 2\)
Therefore, the value of one of the variables is \(x = 2\).
Step 4: Substitute the value of \(x\) in the equation obtained in step 1.
Thus, substituting \(x = 2\) in the equation \(y = 8 - 2x\), we have:
\(y = 8 - 2(2)\)
\(y = 8 - 4 = 4\)
Therefore, the value of the other variable is \(y = 4\).
Hence, the solution of the given system of equations is \(x = 2\) and \(y = 4\).
Verification:
Substitute the solutions \(x = 2\) and \(y = 4\) in equation (\(1\)), we get:
\(\text{LHS} = 2(2) + 4 = 4 + 4 = 8 = \text{RHS}\)
Similarly, substituting \(x = 2\) and \(y = 4\) in equation (\(2\)), we have:
\(\text{LHS} = 2 + 2(4) = 2 + 8 = 10 = \text{RHS}\)
Since in both the equations \(\text{LHS} = \text{RHS}\), \(x = 2\) and \(y = 4\) is the solution to the given equations.
Important!
1. In any of the steps, if we get a false equation like \(0 = 1\), then the system has no solution.
2. If we get an equation like \(0 = 0\), then the system has infinitely many solutions.
Graphical method of solving a pair of linear equation:
The graph of a pair of linear equations in two variables is represented by two lines.
Consistent:
A pair of linear equations in two variables is said to be a consistent system if it has at least one solution.
Inconsistent:
A pair of linear equations in two variables is said to be an inconsistent system if it has no solution.
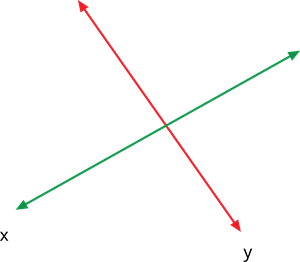
1. When two lines in a graph intersect at only one point, then the graph is a consistent system and has one solution.
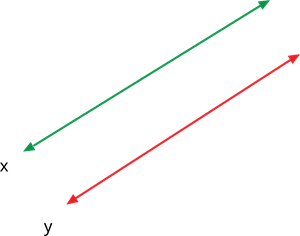
2. When two lines in a graph do not intersect at any point, then the graph is an inconsistent system and has no solution.
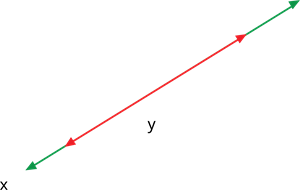
3. When two lines in a graph are identical at all points, the graph is a consistent system and has infinitely many points.
| CONDITION | CONSISTENT OR INCOSISTENT | TYPE OF SOLUTION | GRAPHICAL REPRESENTATION |
| \(\frac{a_1}{a_2}≠\frac{b_1}{b_2}\) | CONSISTENT | UNIQUE SOLUTION | INTERSECTING LINE |
| \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) | CONSISTENT | INFINITELY MANY SOLUTIONS | COINCIDE LINE |
| \(\frac{a_1}{a_2}=\frac{b_1}{b_2}≠\frac{c_1}{c_2}\) | INCONSISTENT | NO SOLUTION | PARALLEL LINE |