Congruence of Triangles:
The property of two or more objects having the exact dimension is called congruence. The objects that exhibit congruence are called congruent figures.
Example:
Let us look at a few examples that exihibit congurence.
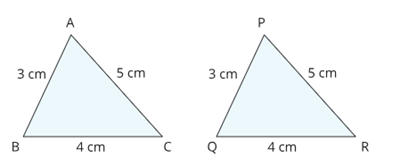

In this session, let us look at the axioms and theorems supporting various congruence criteria.
The four main congruence criterion are:
1. Side - Side - Side (SSS) congruence crietria
2. Side - Angle - Side (SAS) congruence criteria
3. Angle - Side - Angle (ASA) congruence criteria
4. Right angle - Hypotenuse - Side (RHS) congruence criteria
Theorem \(1\) (SSS congruence rule)
If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
Theorem \(2\) (SAS congruence rule)
Two triangles are congruent if to sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
Theorem \(3\) (ASA congruence rule)
Two triangles are congurnet if two angles and the included side of one trianlge are equal to two angles and the included side of the other triangle.
Theorem \(4\) (RHS congruence rule
If in two right angles the hypotenuse and one side of one triangle are equal to the hypoutenuse and one side of the other triangles are congruent.
Some properties of isosceles triangle:
Theorem \(1\)
Angles opposite to equal sides of an isosceles triangle are equal.
Theorem \(2\)
The sides opposite to equal angles of a triangle are equal.