Altitude of a triangle:
The perpendicular line segment drawn from the vertex of a triangle to its opposite side is called the altitude of a triangle.
The altitude of a triangle can be drawn from every vertex of the triangle.
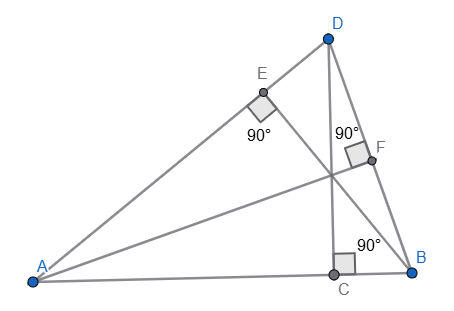
In the above \(\Delta ABD\), the perpendiculars \(AF\), \(BE\), and \(DC\) are altitudes from the vertices \(A\), \(B\), and \(D\) respectively.
How to construct the altitudes of a triangle?
Constructing the altitude precisely using just a ruler is not possible. To get a more precise angle of \(90°\), we use a set square along with a ruler.
We will learn the procedure to construct an altitude from one of the vertex of the triangle.
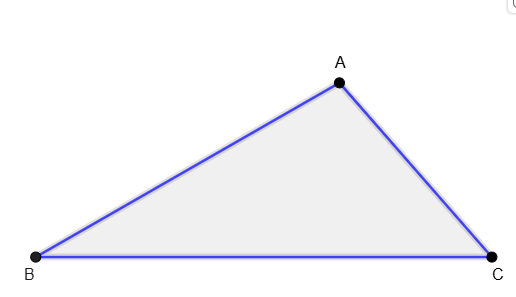
Step - 1: Construct a traingle \(ABC\) of desired measure.
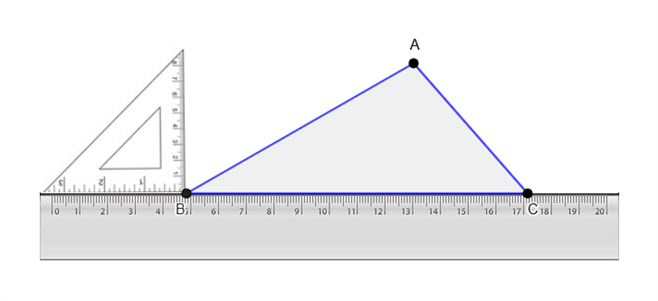
Step - 2: Keep the ruler aligned to the base. Place the set square on the ruler as shown, such that one of the edges of the right angle touches the ruler.
Step - 3: Slide the set square along the ruler till the vertical edge of the set square touches the vertex \(A\).
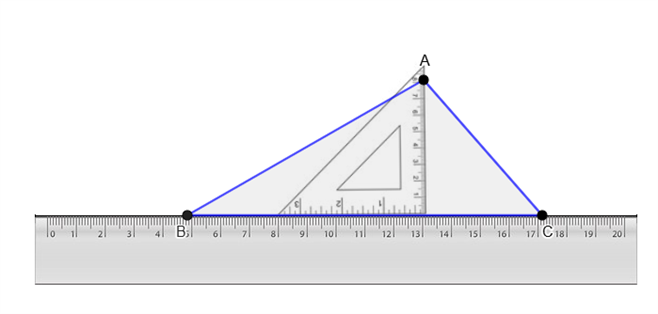
Step - 4: Draw the altitude to \(BC\) through \(A\) using the vertical edge of the set square.
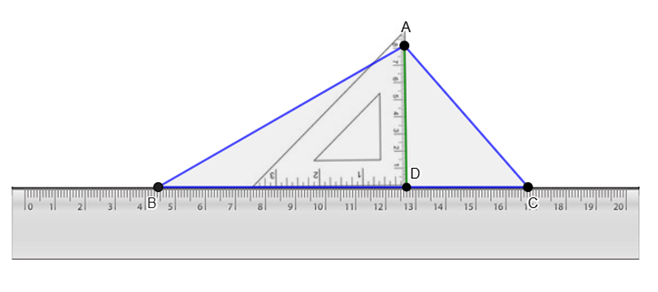
Thus, the perpendicular line segment \(AD\) is the required altitude from \(A\).