Let us learn how to construct a triangle if the measures of \(2\) of its angles and the length of the side included between them are known.
Procedure to construct a triangle:
Let us constructs a \(\Delta ABC\)(say) with \(AB = x \ cm\), \(\angle A = y^{\circ}\), and \(\angle B = z^{\circ}\).Step - 1: Construct the base line segment \(AB = x \ cm\).
Step - 2: Place the protractor at \(A\) and construct \(\angle A = y^{\circ}\) by drawing the other arm of the angle.
Step -3: Place the protractor at \(B\) and construct \(\angle B = z^{\circ}\) by drawing the other arm of the angle.
Step - 4: Mark the intersecting point of the two arms as the vertex \(C\). Thus, \(\Delta ABC\) is the required triangle.
Step - 2: Place the protractor at \(A\) and construct \(\angle A = y^{\circ}\) by drawing the other arm of the angle.
Step -3: Place the protractor at \(B\) and construct \(\angle B = z^{\circ}\) by drawing the other arm of the angle.
Step - 4: Mark the intersecting point of the two arms as the vertex \(C\). Thus, \(\Delta ABC\) is the required triangle.
Example:
Construct a triangle \(ABC\) whose measurements are \(AB = 8 \ cm\), \(\angle CAB = 60^{\circ}\) and \(\angle ABC = \angle 40^{\circ}\).
Construction:
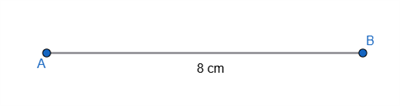
Step 1: Draw a line segment \(AB\) of length \(8 \ cm\).
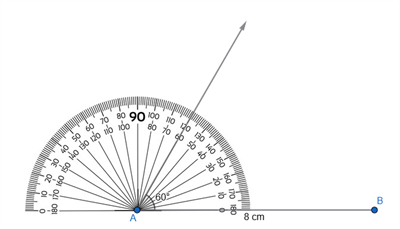
Step 2: Place the protractor at \(A\) and construct \(\angle A = 60^{\circ}\) by drawing the other arm of the angle.
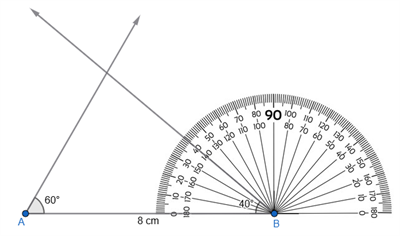
Step 3: Place the protractor at \(B\) and construct \(\angle B = 40^{\circ}\) by drawing the other arm of the angle.
Step 4: Mark the intersecting point of the two arms as the vertex \(C\).
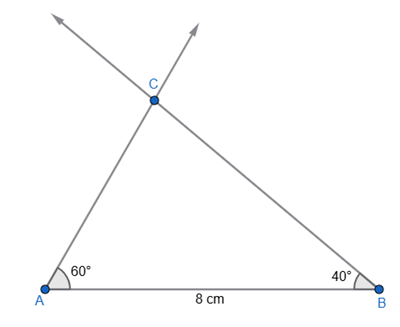
Therefore, \(ABC\) is the required triangle.