Prove that \(\angle ACD = \angle A + \angle B\) using the properties of parallel lines.
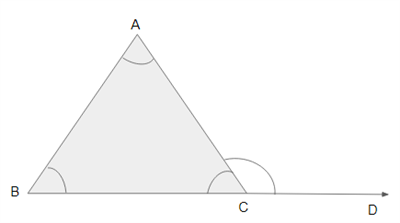
Proof:
Construct a line \(CE\) parallel to \(AB\).
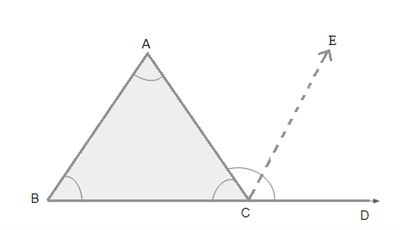
If \(AC\) is the transversal, then \(∠A = ∠ACE\) .....(1) [Since ]
If \(BD\) is the transversal, then \(∠B=∠ECD\) ......(2) [Since ]
\(∠ACD = ∠ACE + ∠ECD\) []
From equation (1) and (2), \(∠ACD = ∠A + ∠B\).
Hence, proved.