Exterior angle of a triangle:
The angle formed between the extension of one side of a triangle and its corresponding side is called an exterior angle of the triangle.
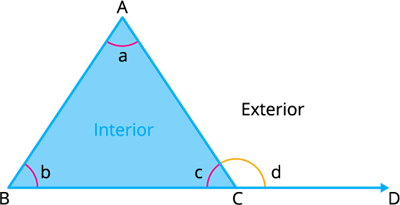
In this figure, for the vertex \(C\), the interior angle is \(∠ACB = c\) and the exterior angle is \(∠ACD = d\).
Forms of exterior angles in a triangle:
Exterior angles can be formed for a triangle in many ways. They are as follows:
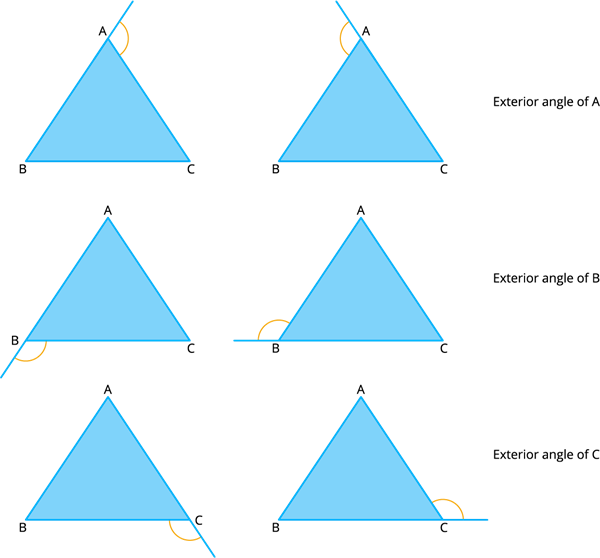
Enterior angle property:
Statement:
An exterior angle of a triangle is equal to the sum of its opposite interior angles.
By the property, we can \(\angle ACD = \angle ABC + \angle BAC\)
\(\Rightarrow\) \(d = a + b\)
Proof:
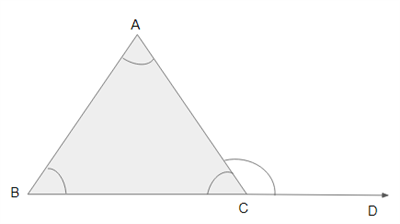
Given:
Consider a triangle \(ABC\) with extended line \(CD\) forms an exterior angle to vertex \(C\).
To prove:
\(∠ACD\) \(=\) \(∠BAC\) \(+\) \(∠ABC\)
Proof:
We will prove this using the angle sum property of the triangle.
The angle sum property states that,
The sum of the measure of three angles of a triangle is \(180°\).
By the property, \(\angle BAC + \angle ABC + \angle ACB = 180°\) ..........(1)
Consider the line \(BD\).
Here, \(\angle ACB\) and \(\angle ACD\) are linear angles.
We know that,
The sum of all angles on a straight line is \(180°\).
\(\Rightarrow\) \(\angle ACB + \angle ACD = 180°\) ..........(2)
Equating (1) and (2), we have:
\(\angle BAC + \angle ABC + \angle ACB = \angle ACB + \angle ACD\)
\(\angle BAC + \angle ABC + \angle ACB - \angle ACB = \angle ACD\)
\(∠BAC\) \(+\) \(∠ABC\) \(=\) \(\angle ACD\)
Hence, the proof.