What is a magic square?
A magic square is a grid with numbers arranged so the row, column, and diagonal sums are all the same.
In a \(3×3\) magic square with numbers \(1 - 9\), the magic sum is always \(15\).
Which Numbers Can Be in the Center?
The middle number is a part of \(4\) lines (row, column, and \(2\) diagonals).
So, only \(5\) works in the center.
Why \(9\) or \(1\) does not work in the center?
If center equals \(9\), you'd need a row like \(9 + 8 +\) another number \(= 15\), which is not possible.
Similarly, \(1 + 2 +\) other number \(= 15\), which is not possible.
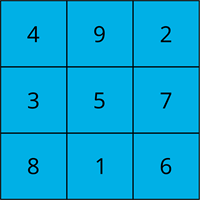
Arranging Numbers:
- \(1\) and \(9\) cannot be in a corner in a magic square. They must be in the middle of an edge.
- \(5\) always in the centre of the grid.
- Opposite cells always add to \(10\) (e.g. \(2 & 8\), \(3 & 7\))
- Each row, column, and diagonal totals \(15\).w
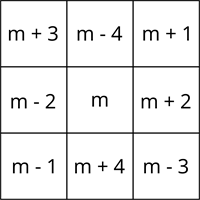
General form of \(3 \times 3\) magic square:
Let the centre of the grid be \(m\).
A \(3 \times 3\) magic square built from consecutive numbers has this pattern relative to the center.