Transversal is a line, which intersects two or more lines in different points.

Here, \(m\) and \(n\) are any two non-parallel lines and \(l\) is another line intersecting them at \(A\) and \(B\).
Such intersecting line (\(l\)) is called as a transversal line because the line \(l\) intersects two lines at distinct points.
Types of angles:
If a transversal line meets two lines (parallel or unparalleled lines), \(8\) angles are formed at the points of intersection as shown in the below figure.

1. Corresponding angles
2. Vertically opposite angles
3. Interior angles
4. Alternate angles
Let us discuss the different types of angles briefly.
1. Corresponding angles:
Consider the pair of angles \(\angle 1\), \(\angle 5\); \(\angle 2\), \(\angle 6\); \(\angle 3\), \(\angle 7\) and \(\angle 4\), \(\angle 8\) are corresponding angles.
Corresponding angles formed by a transversal intersecting a pair of parallel lines are always equal to each other.
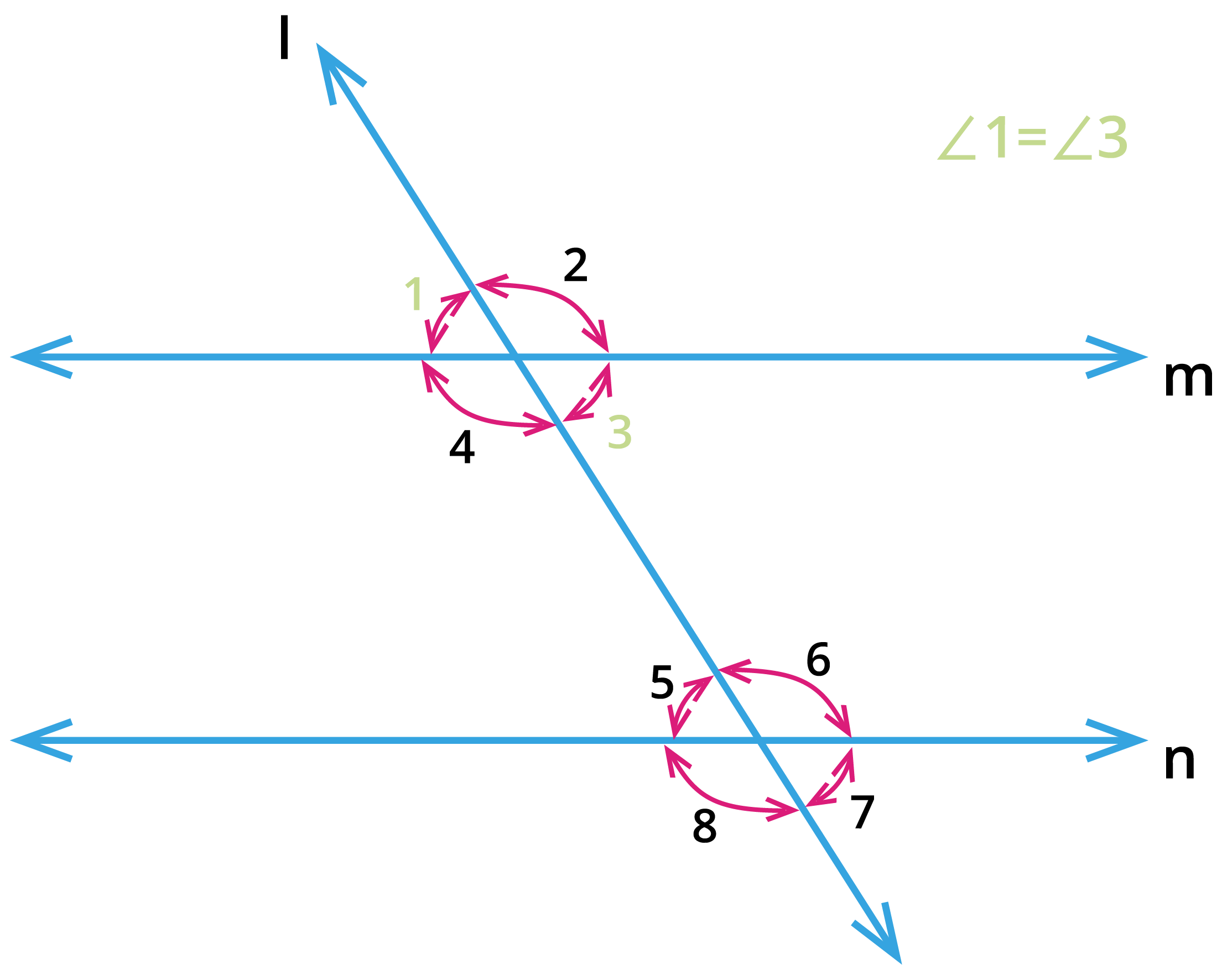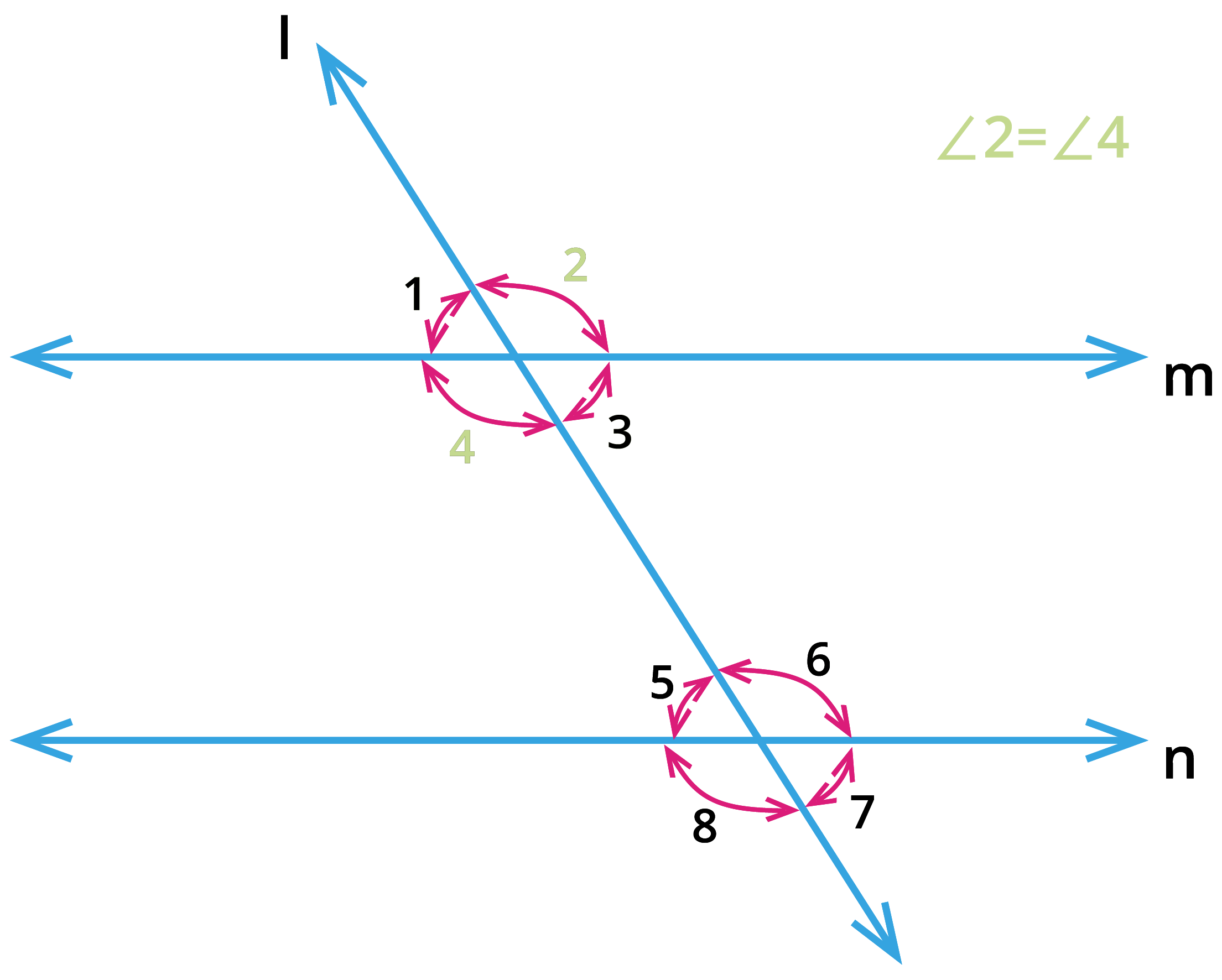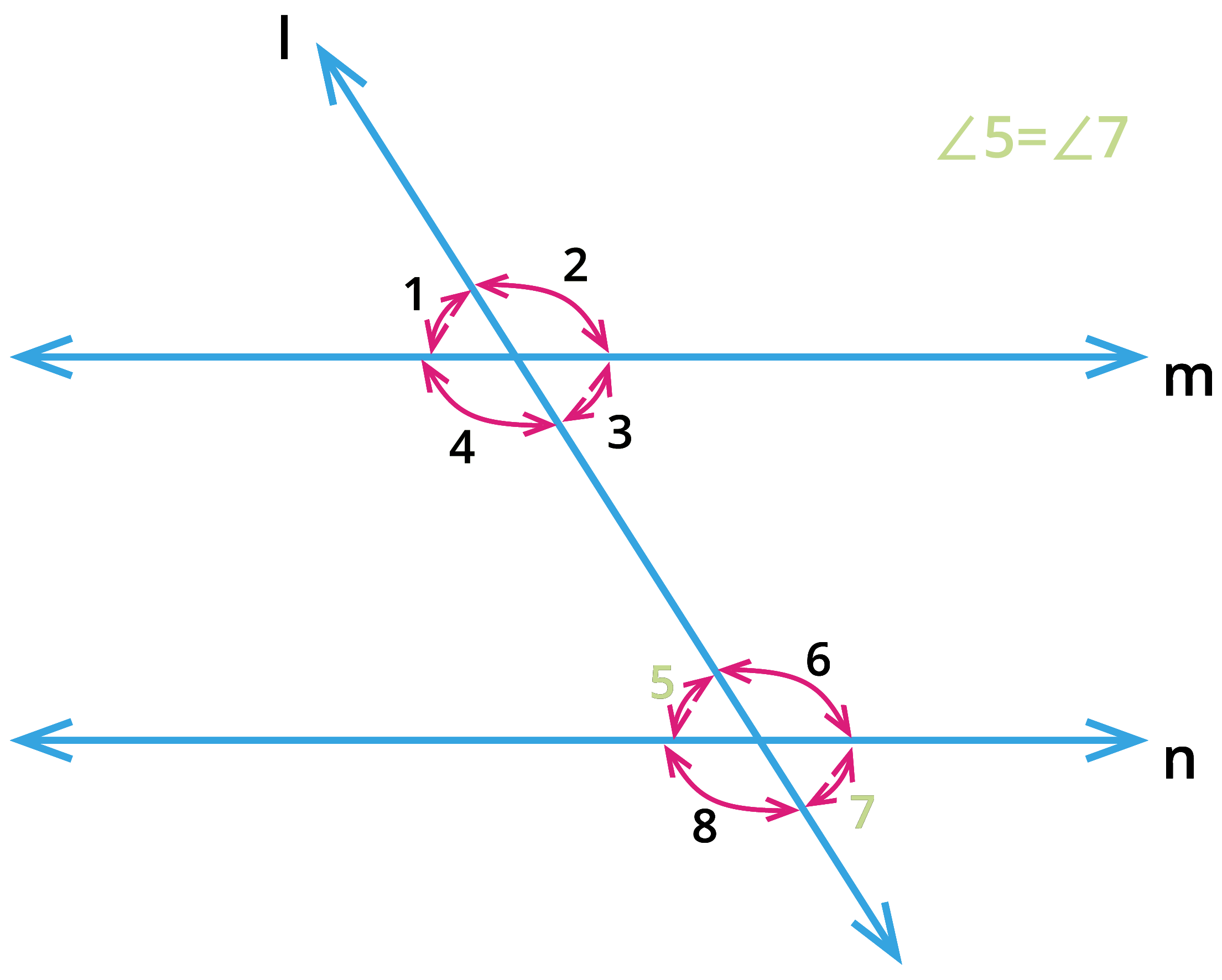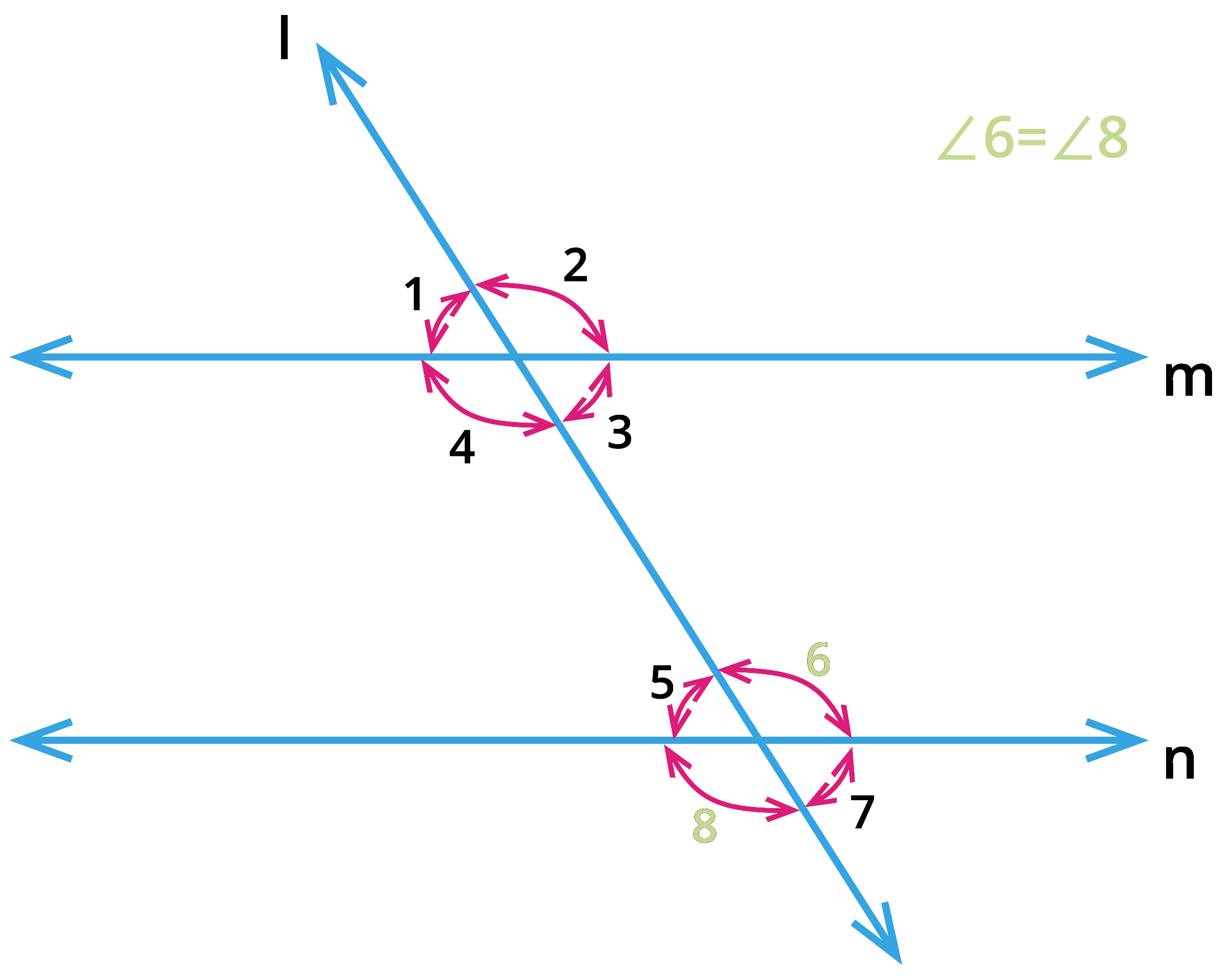
2. Vertically opposite angles:
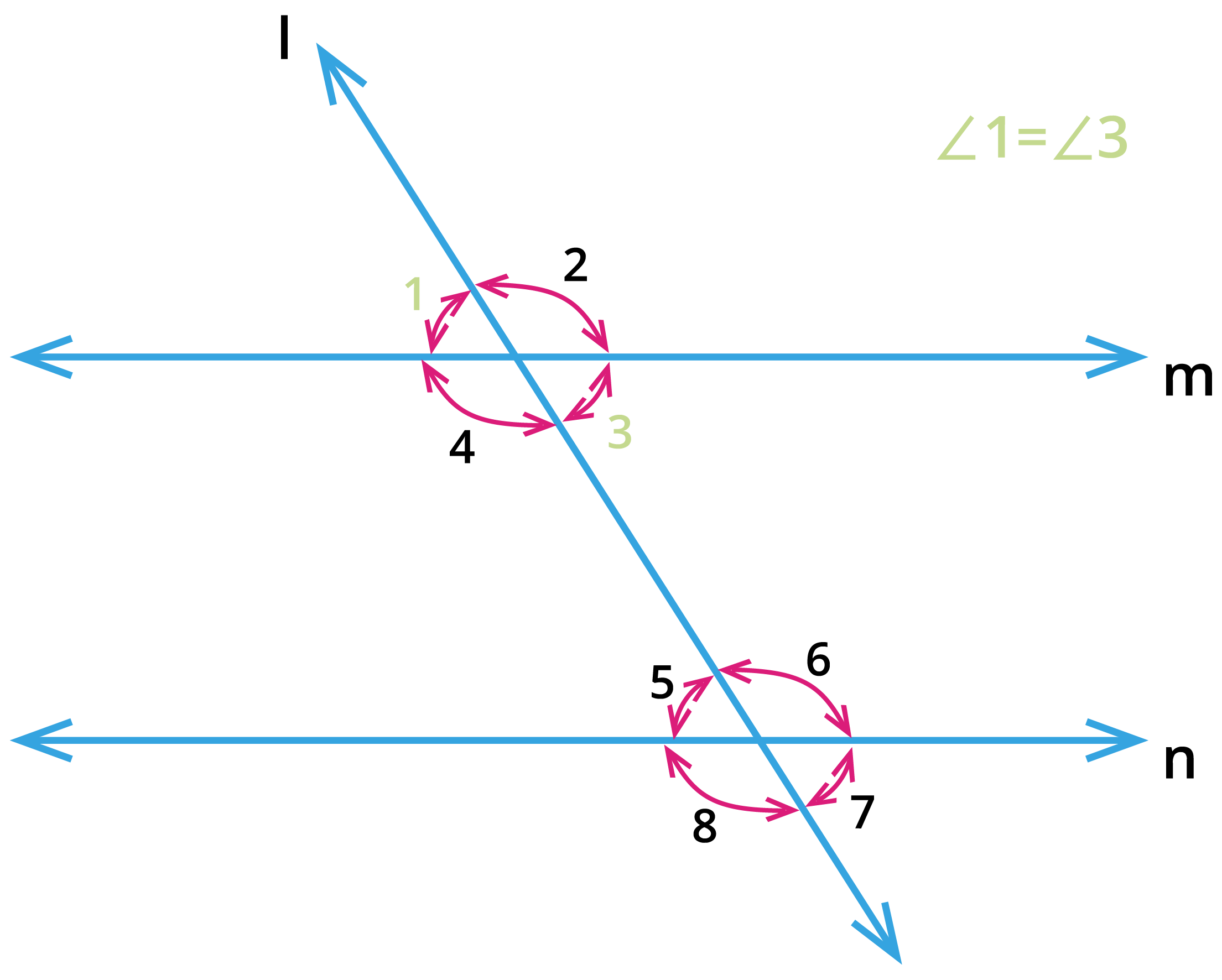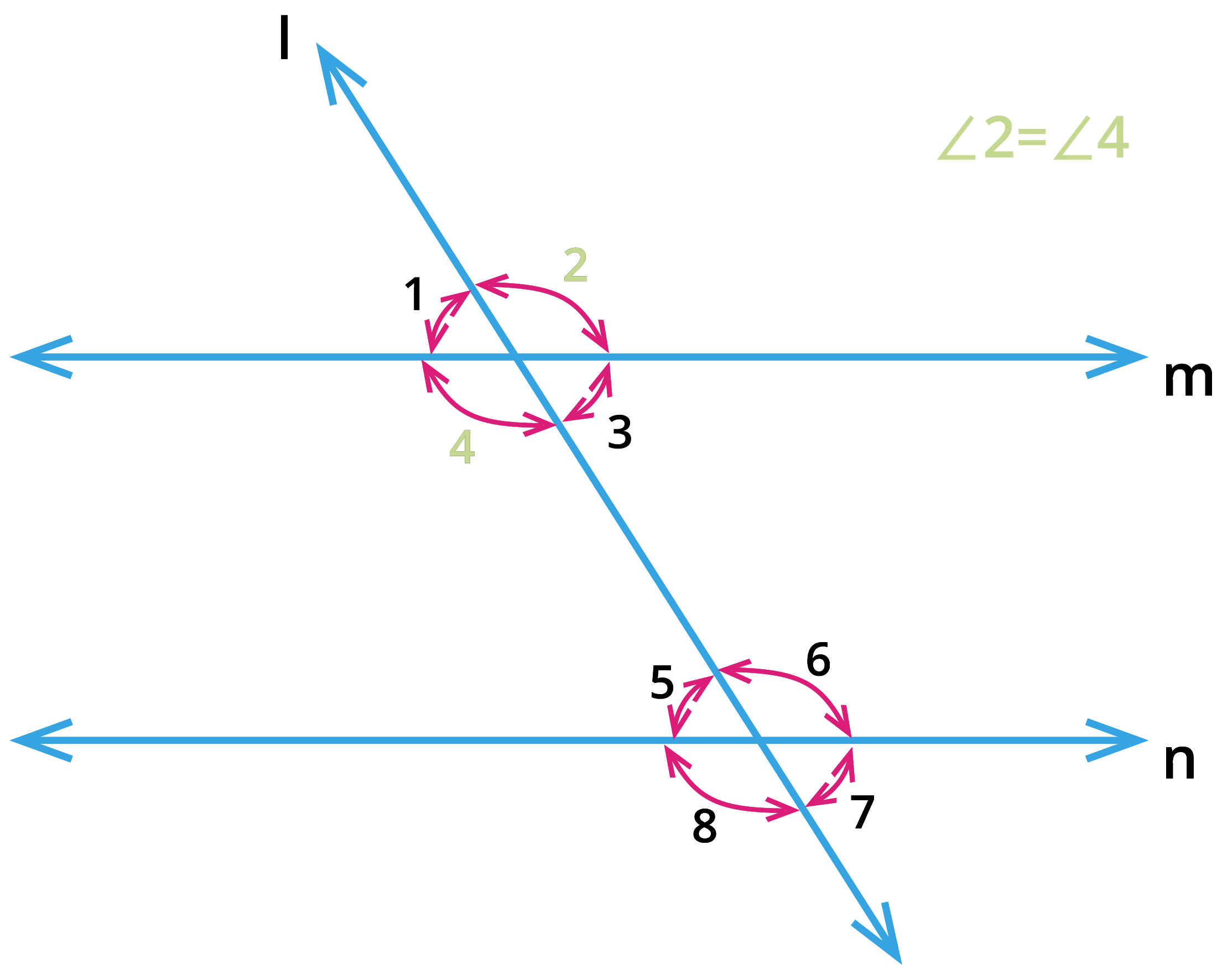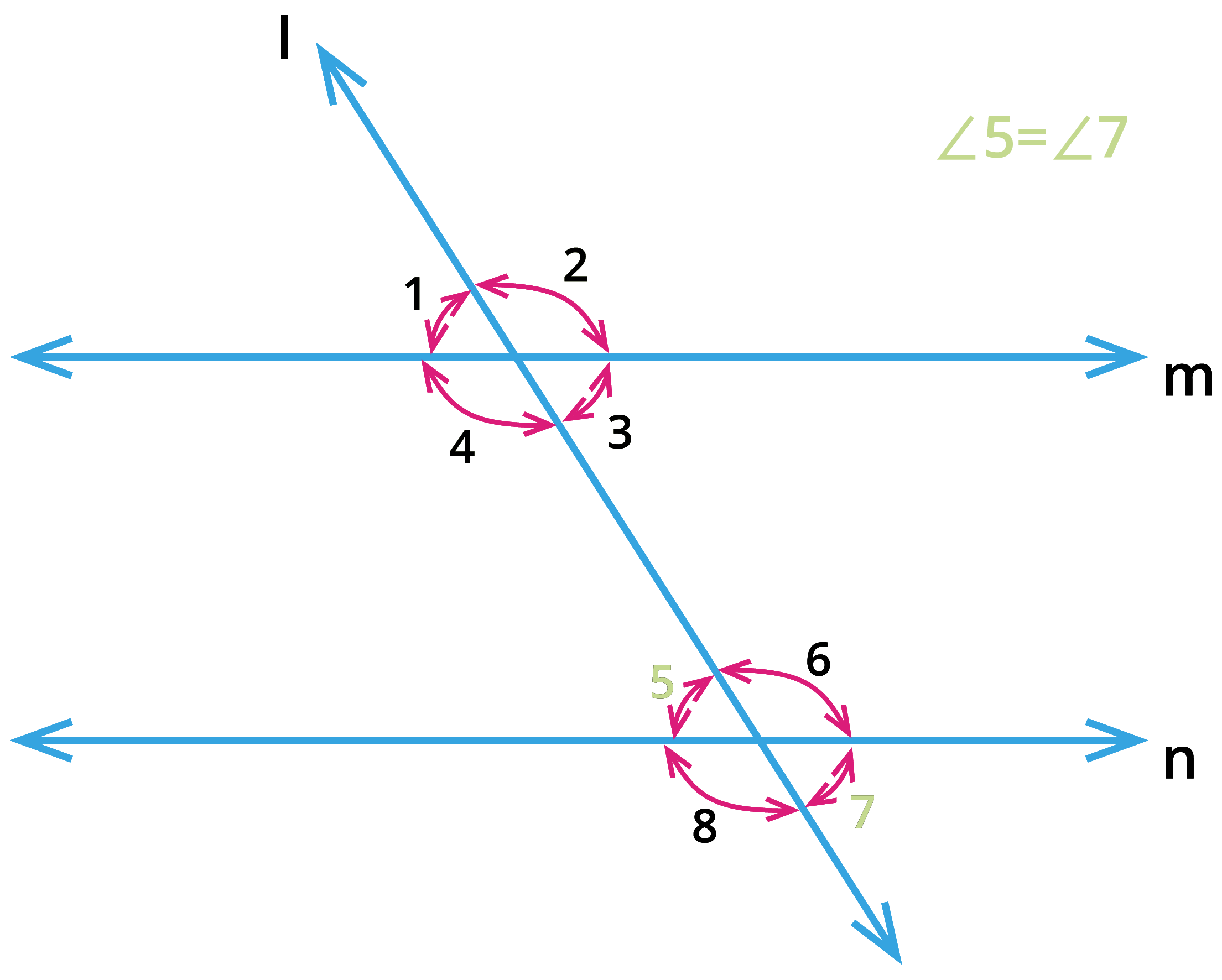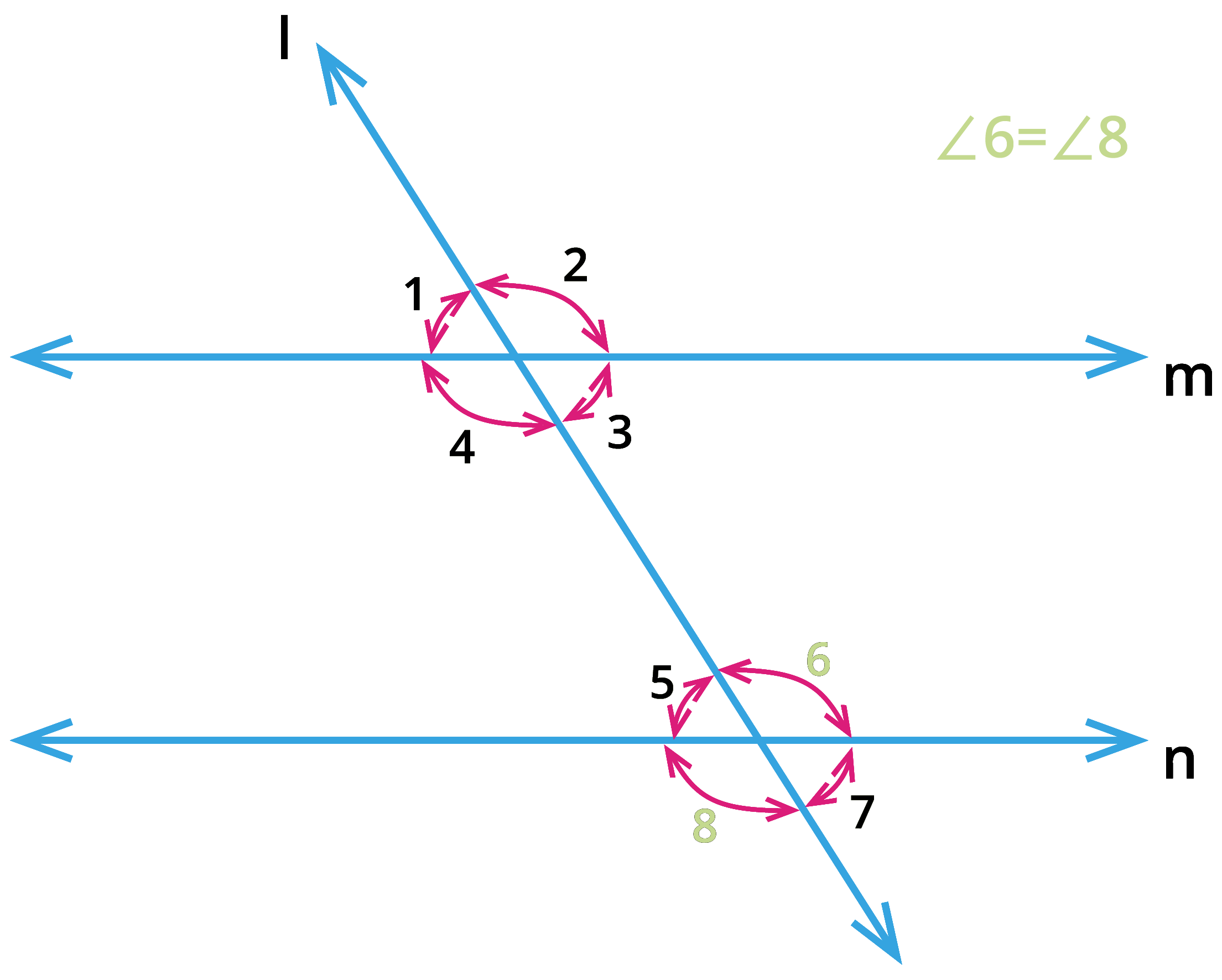
From the above figure, consider the pair of angles \(\angle 1\), \(\angle 3\); \(\angle 2\), \(\angle 4\); \(\angle 5\), \(\angle 7\) and \(\angle 6\), \(\angle 8\). These pair of angles share the same vertex and they are opposite to each other. These pair of angles are called as vertically opposite angles and the opposite angles are equal.
3. Interior angles:
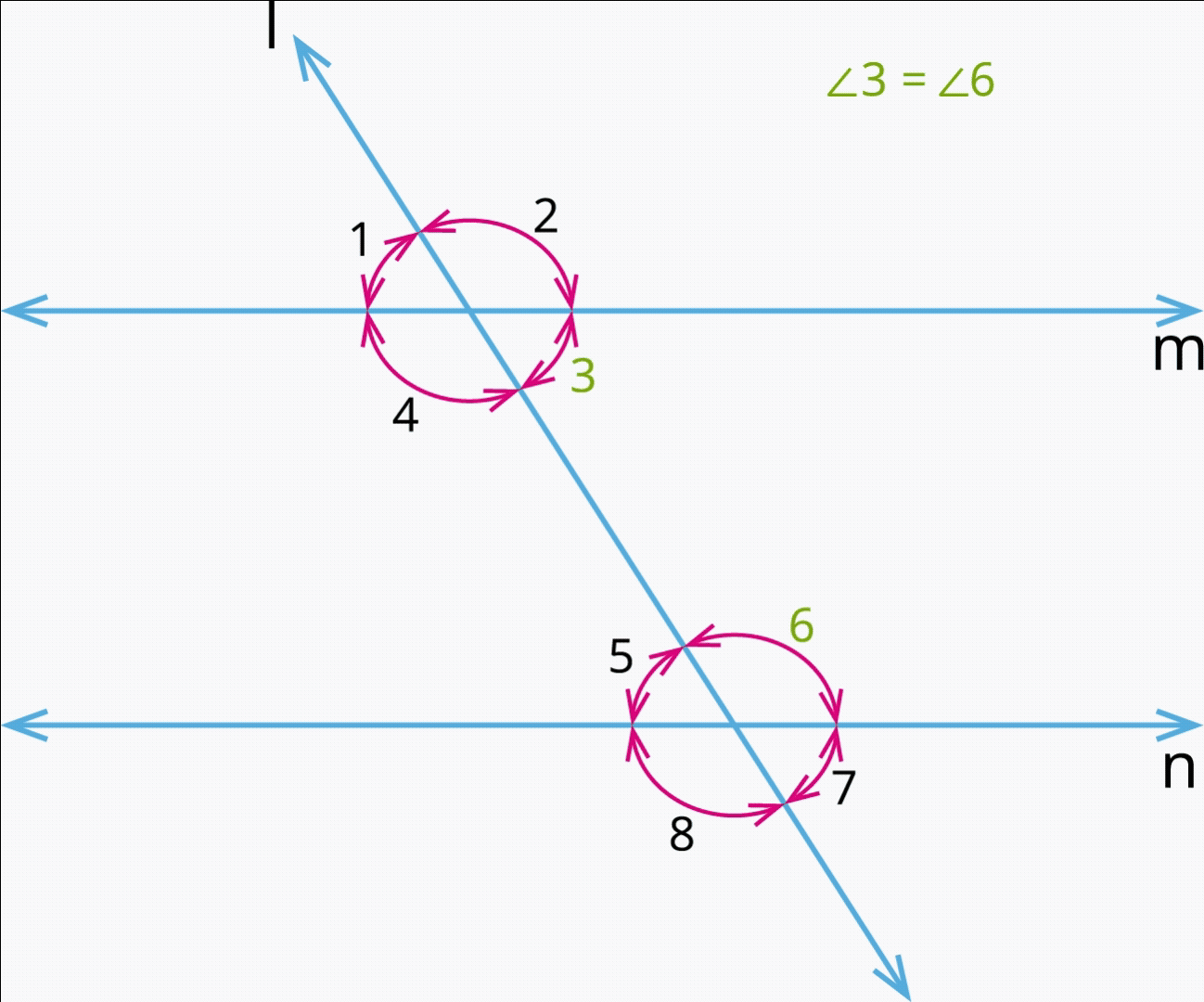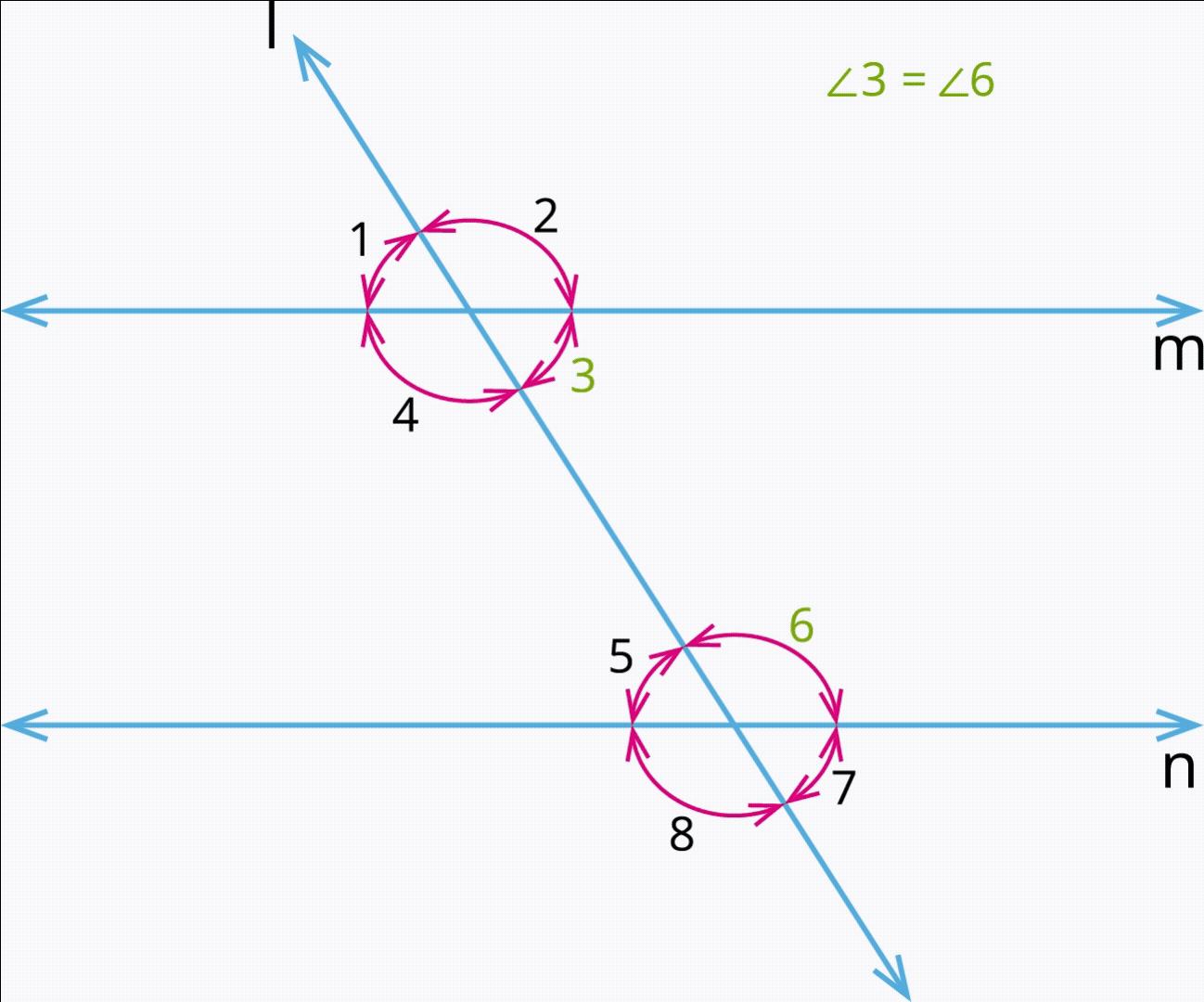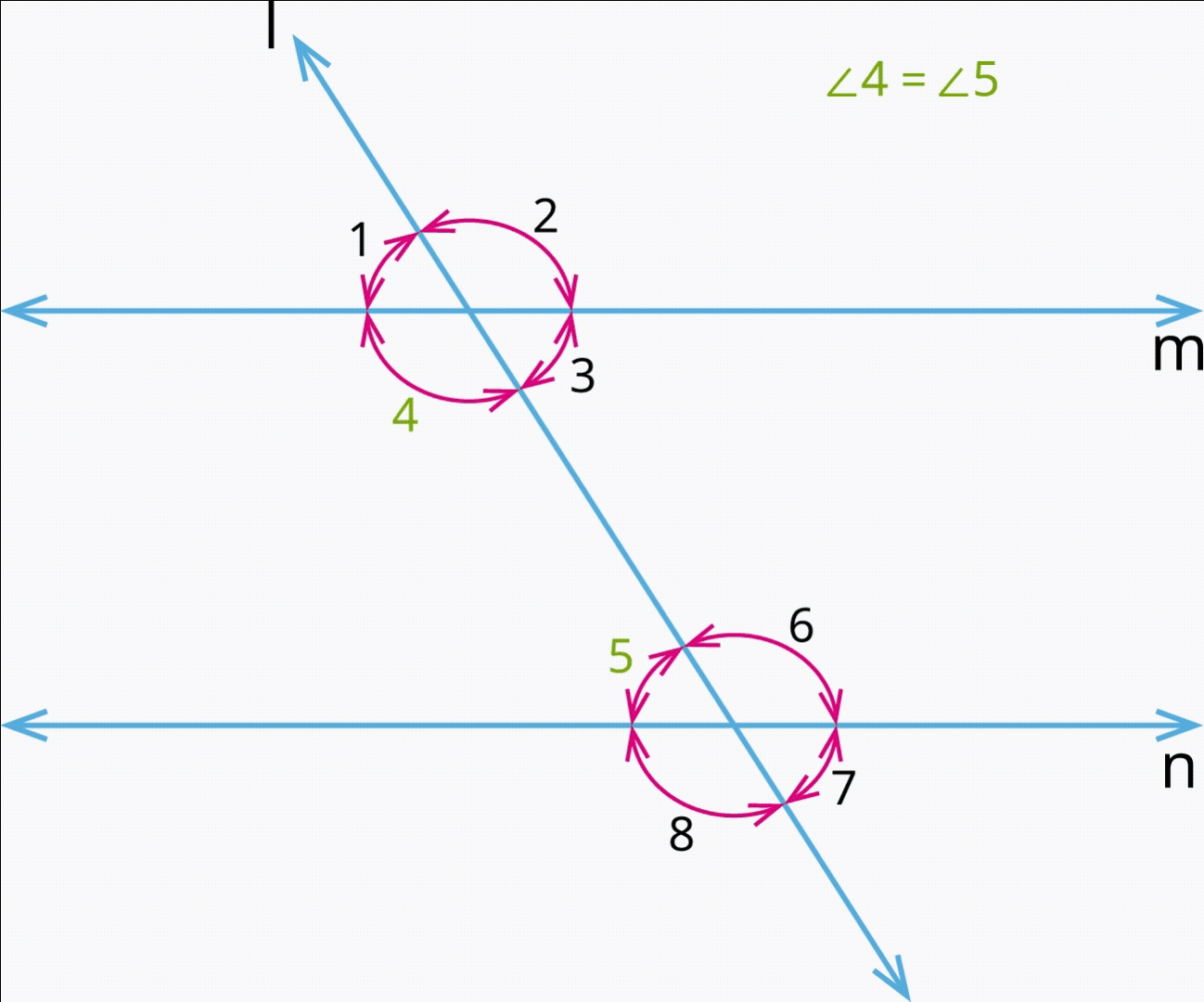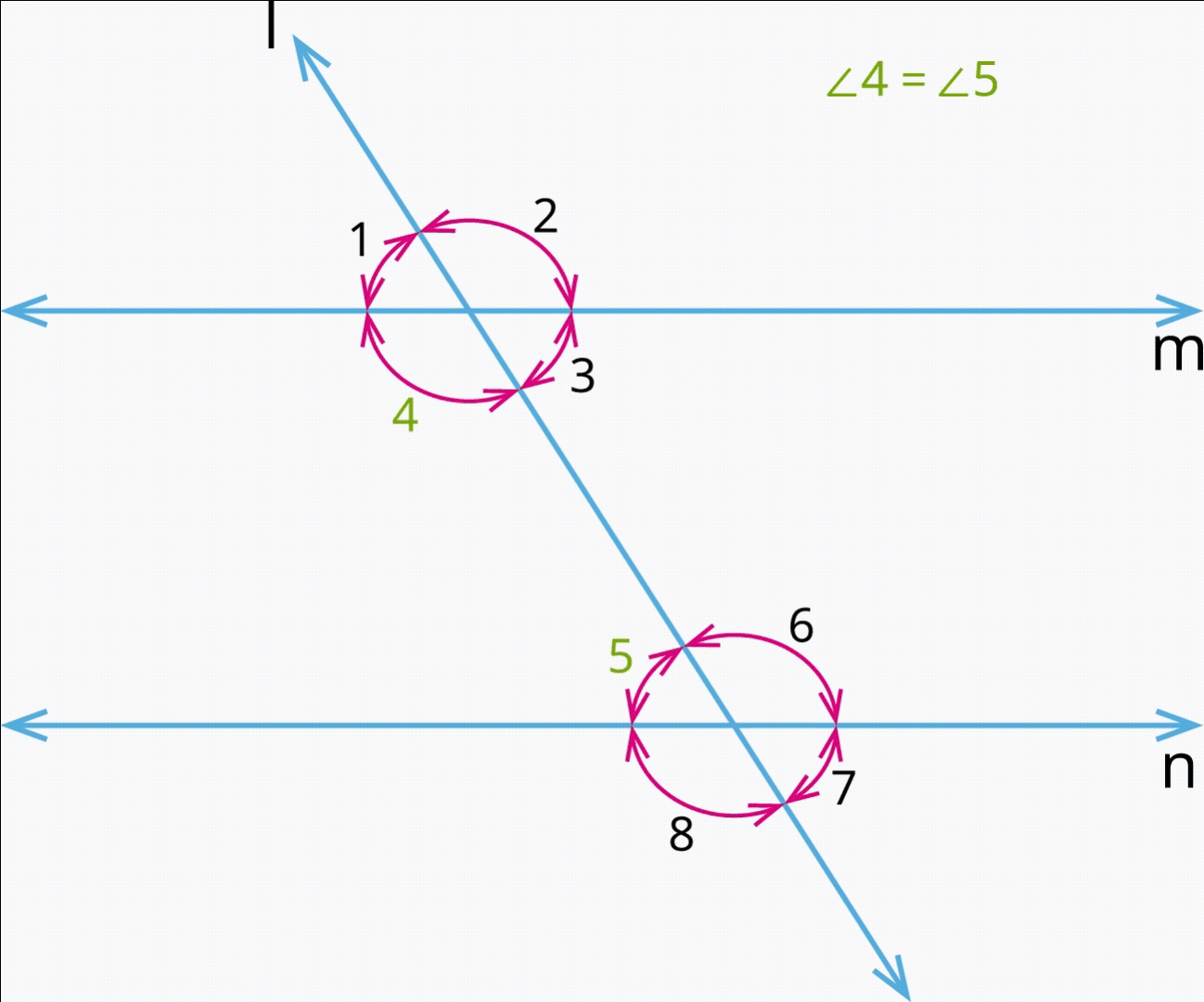
Consider the pair of angles \(\angle 3\), \(\angle 6\); \(\angle 4\), and \(\angle 5\) are interior angles.
4. Alternate interior angles:
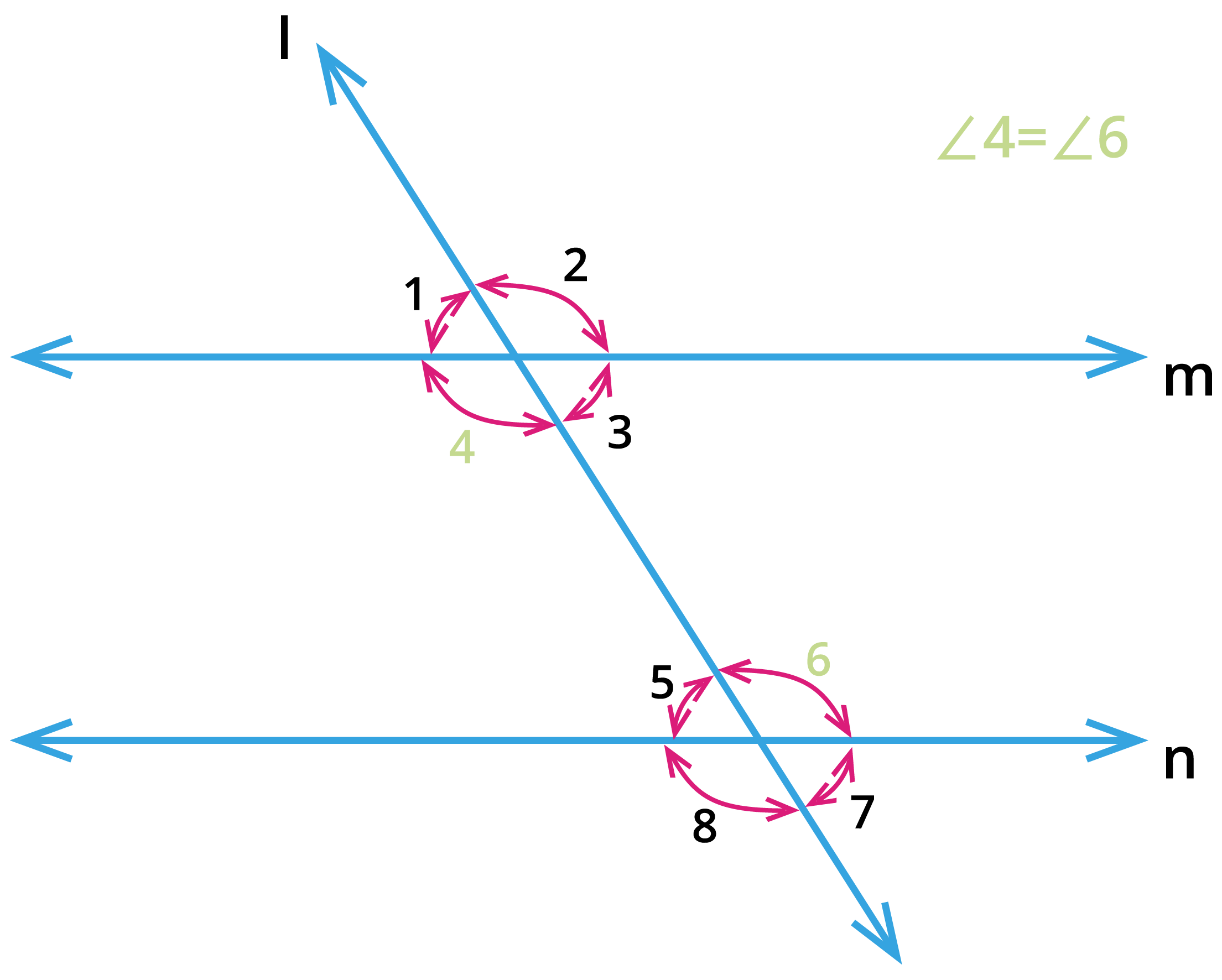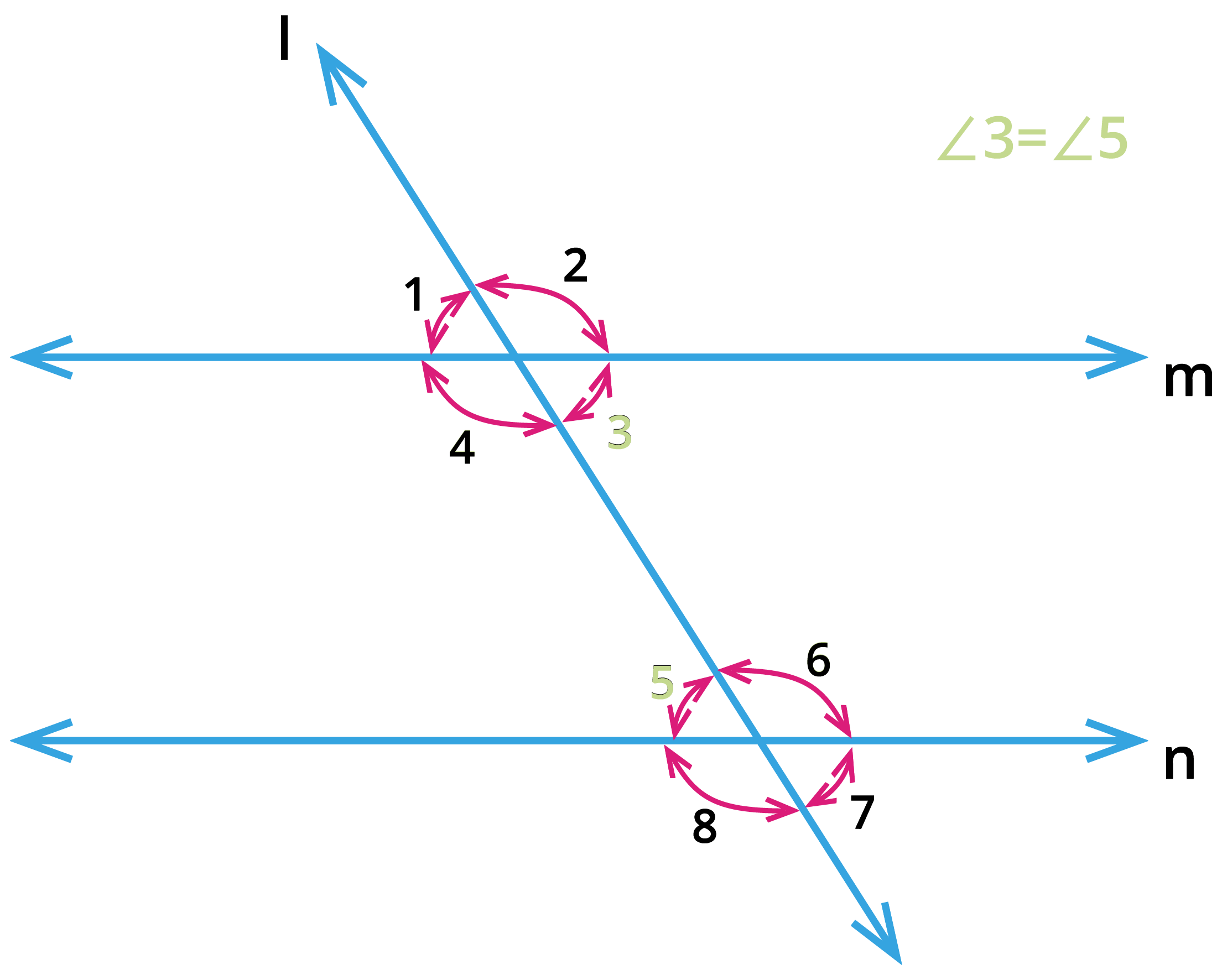
Consider the pair of angles \(\angle 4\), \(\angle 6\) and \(\angle 3\), \(\angle 5\) are alternate interior angles.
5. Alternate exterior angles:
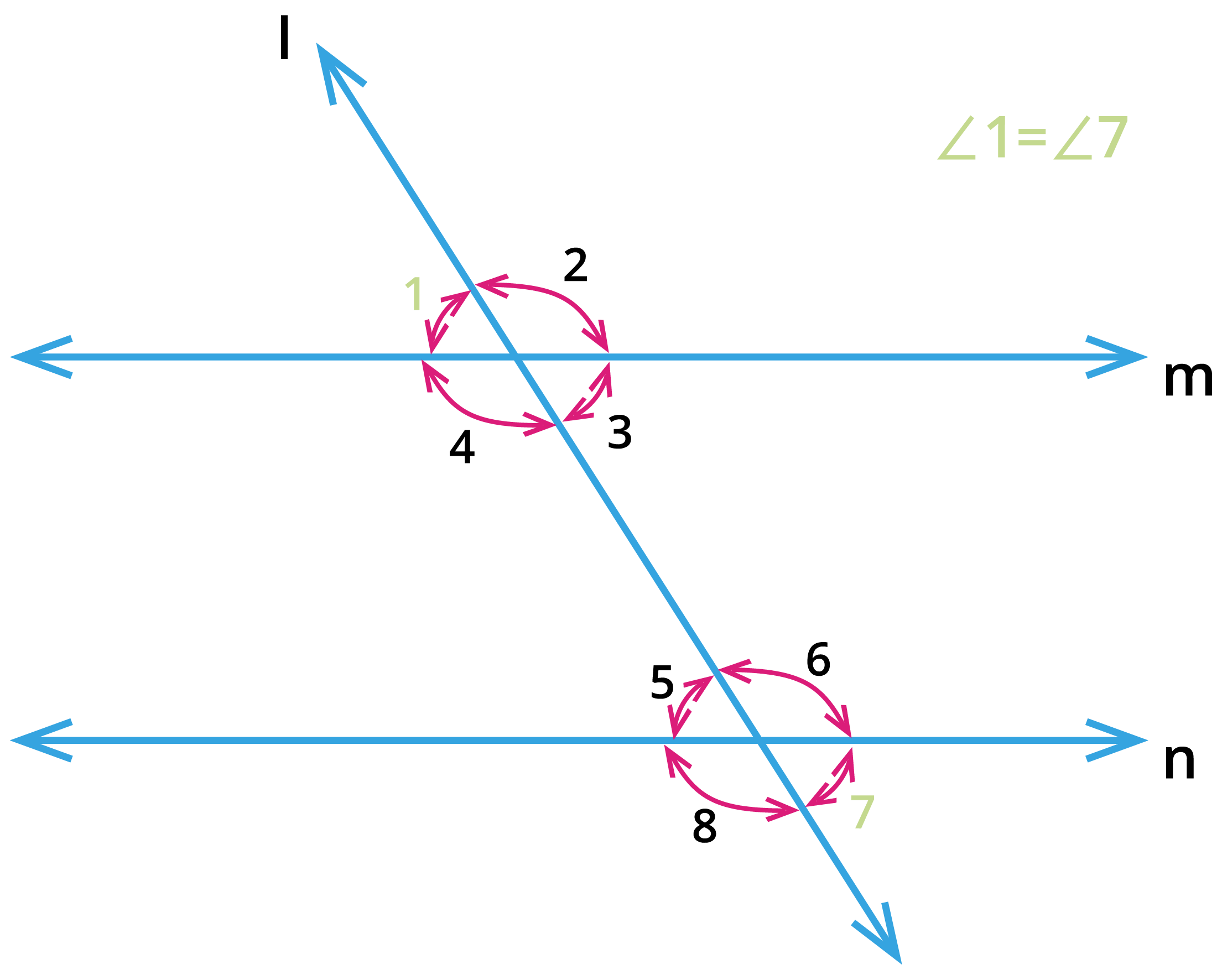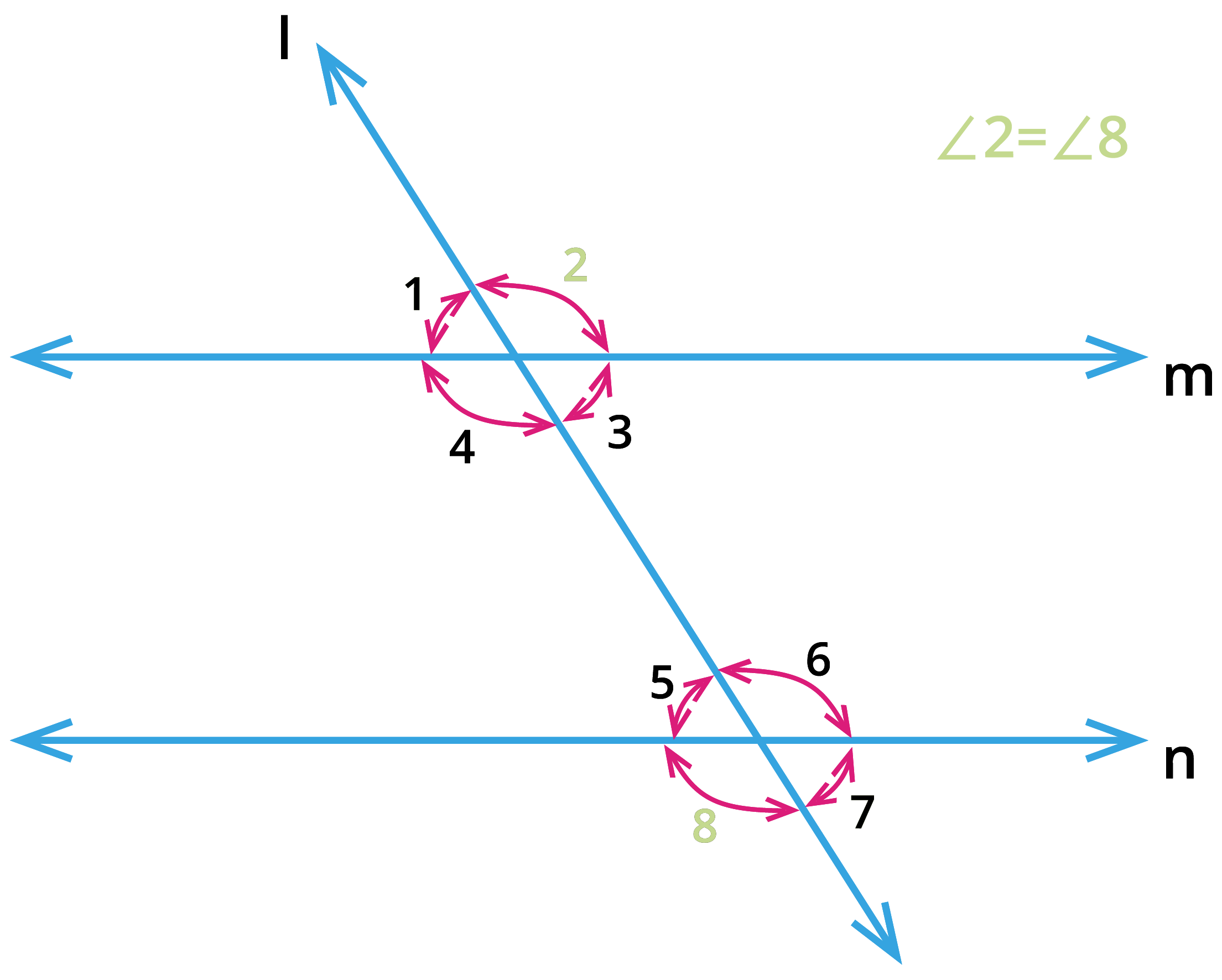
Consider the pair of angles \(\angle 1\), \(\angle 7\) and \(\angle 2\), \(\angle 8\) are alternate exterior angles.
Important!
1. When a pair of lines are not parallel to each other, the corresponding angles formed by a transversal can never be equal to each other.
2. When a line t intersects another pair of lines, it is called a transversal and it forms \(2\) sets of \(4\) angles. Each of the \(4\) angles in the first set has a corresponding angle in the second set.
3. When a transversal intersects a pair of parallel lines, the corresponding angles are equal. When a transversal intersects a pair of lines and the corresponding angles are equal, then the pair of lines is parallel.
4. When a transversal intersects a pair of parallel lines, the alternate angles are equal.
5. The interior angles on the same side formed by a transversal intersecting a pair of parallel lines always add up to 180°.