Multiplying two fractions:
To multiply two fractions we have two methods,
(i) Unit square method
(ii) Formula method
Unit square method
Steps to find multiplying of fractions using unit square
Step 1:
Consider the \(\text{first}\) fraction,
Dividing the unit square into many vertical strips as indicated as the denominator of the given fraction.
Step 2:
Consider the \(\text{second}\) fraction,
Dividing the unit square into many horizontal strips as indicated as the denominator of the given fraction.
Step 3:
To mutliply both the fraction,
We need to \(\text{overlap}\) both the above unit sqaures together in step 1 and step 2.
Then the solution would be,
The product of the given fraction found by the number of overlapping rectangles divided by the over all rectangles.
Example:
Solve \(\frac{1}{3} \times \frac{1}{5}\), using unit square as a whole for the representing fraction.
Solution:
Fraction \(\frac{1}{3}\) represented by the unit square is,

Fraction \(\frac{1}{5}\) represented by the unit square is,

Thus, \(\frac{1}{3} \times \frac{1}{5}\) represented by the unit square is,
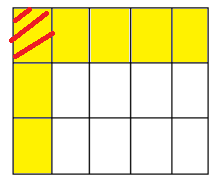
The product of the given fraction found by the number of overlapping rectangles divided by the over all rectangles.
Hence, \(\frac{1}{3} \times \frac{1}{5} = \frac{1}{15}\)
Important!
While representing fraction in unit square, one fraction should take vertical strips and another fraction should take vertical strips. Both should not take the same direction strips.
Formula method:
If there are two fractions \(\frac{a}{b}\) and \(\frac{c}{d}\), multiplying those two fractions refers multiplying the numerators together and denominators together.
\(\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\)
Example:
Solve \(\frac{1}{3} \times \frac{1}{5}\)
Solution:
To solve the above fraction \(\frac{1}{3} \times \frac{1}{5}\) we can use the formula,
\(\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\)
Thus we get,
\(\frac{1}{3} \times \frac{1}{5}\)
\(=\frac{ 1 \times 1}{3 \times 5}\)
\(= \frac{1}{15}\)
Important!
In both the ways, we will get the same answer.