Is the product always greater than the numbers multiplied?
We know that, when a number multiplied by \(1\), the product remains unchanged.
Similarly we have some suituation as follows,
When we multiply two numbers which are greater than \(1\), the product is greater than both the numbers being multiplied.
Consider a number between \(0\) and \(1\) and one number is greater than \(1\), then their product is greater than the number between \(0\) and \(1\), and lesser than the number greater than \(1\).
Consider two numbers between \(0\) and \(1\), then their product is lesser than those two numbers
Division of Fractions:
If one fraction is divided by another fraction the below formula will be used,
\(\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}\)
Fractional Relations:
Let us understand this topic using the below example.
Here is the square with some lines
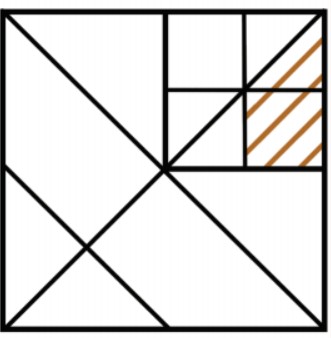
We need to find the fraction of a area of the whole square that is shaded.
Let the area of the whole square be \(1\) square unit.
From the figure we get, the top right square occupies \(\frac{1}{4}\) of the whole square.
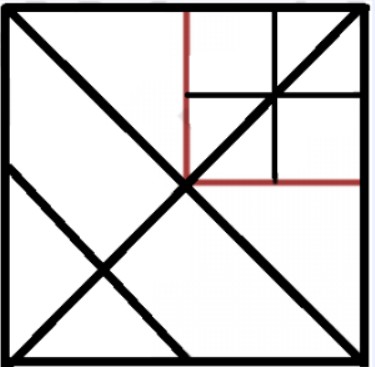
Area of above top right square = \(\frac{1}{4}\) square units.
We can split the above square in this below way,
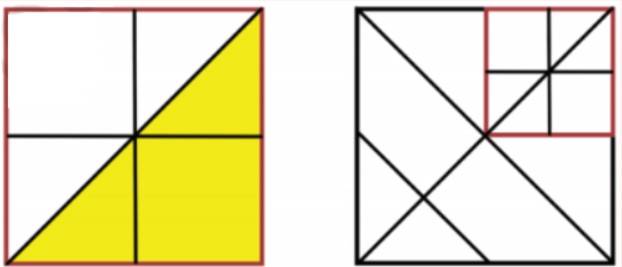
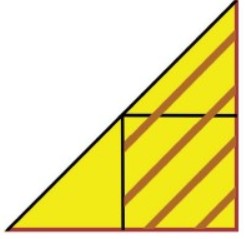
This yellow shade is detailed explanation of above figure.
Area of yellow triangle \(= \frac{1}{2} \times \frac{1}{4} = \frac{1}{8} \text{square units}\)
The shaded region in the question occupies \(\frac{3}{4}\) space in yellow region
Thus the area of shaded region \(= \frac{3}{4} \times \frac{1}{8} = \frac{3}{32} \text{square units}\)