Look at the pattern below carefully.

In the above pattern:
The first picture has \(1\) row and \(1\) column.
The second picture has \(2\) rows and \(2\) columns.
The third picture has \(3\) rows and \(3\) columns.
The fourth picture has \(4\) rows and \(4\) columns.
\(1 \times 1 = 1^2 = 1\)
\(2 \times 2 = 2^2 = 4\)
\(3 \times 3 = 3^2 = 9\)
\(4 \times 4 = 4^2 = 16\)
Here, we multiply the number by itself, and we obtained a square of that number.
The numbers \(1\), \(4\), \(9\) and \(16\) are called square numbers.
If a natural number \((m)\) is expressed as a power of \(2\), then the number \((m)\) is called a square number. That is \(m = n^2\).
A perfect square is a number that can be expressed as the product of an integer by itself. For example, \(25\) is a perfect square because it is the product of integer \(5\) by itself, \(5 × 5 = 25\). However, \(21\) is not a perfect square number because it cannot be expressed as the product of two same integers.
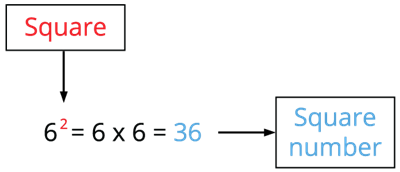
We know that the inverse (opposite) operation of addition is subtraction and the inverse operation of multiplication is division.
Similarly, finding the square root is the inverse operation of squaring.
That is, the square root is the inverse operation of a square.
The square root of a number is represented by the symbol .
The square root of a number \(n\) can be written as \(\sqrt{n}\).
Example:
1. The square of \(2\) is \(4\). That is \(2^2 = 4\).
The square root (inverse) of \(4\) is \(2\). That is \(\sqrt{4} = 2\).
2. The square of \(5\) is \(25\). That is \(5^2 = 25\).
The square root (inverse) of \(25\) is \(5\). That is \(\sqrt{25} = 5\).
1. The square numbers end in \(0\), \(1\), \(4\), \(5\), \(6\) or \(9\) only.
2. If a number ends with \(1\) or \(9\), its square ends with \(1\).
3. If a number ends with \(2\) or \(8\), its square ends with \(4\).
4. If a number ends with \(3\) or \(7\), its square ends with \(9\).
5. If a number ends with \(4\) or \(6\), its square ends with \(6\).
6. If a number ends with \(5\) or \(0\), its square also ends with \(5\) or \(0\), respectively.
7. Square of an odd number is always odd, and the square of an even number is always even.
8. Numbers that end with \(2\), \(3\), \(7\) and \(8\) are not perfect squares.
9. The sum of the first \(n\) consecutive odd natural numbers is \(n^2\).
10. Count of numbers between \(n^ 2\) and \((n + 1)^ 2 = 2n\).
To check whether the given natural number is a perfect square or not, we can follow the steps below:
Step 1. Write the given natural number as a product of prime factors.
Step 2. Now, group the factors in pairs so that both factors in each pair are equal.
Step 3. Now, see whether some factors are leftover or not. If no factor is left over in grouping, then the given number is a perfect square. Otherwise, it is not a perfect square.
Step 4. Take one factor from each group and multiply them to obtain the number whose square is the given number.