1. Introduction:
- These strange symbols are one of the ways of writing numbers around 4000 years ago in a region called Mesopotamia
- Ancient Indian text, such as \(\text{Yajurveda Samhita}\) has mentioned number names based on the powers of 10.
Examples:
\(\text{one}\) = eka
\(\text{ten}\) = dasha
\(\text{hundred}\) = shata
\(\text{thousand}\) = sahasra
\(\text{ten thousand}\) = ayuta etc.,
- The structure of the modern oral and written numbers that we use today had its origin thousands of years ago in India.
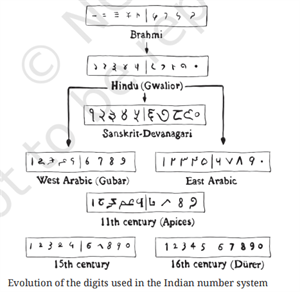
2. Shapes of digits:
The shapes of digits 0,1,...,9 we used to write numbers in the Indian number system today evolved over period of time, as shown below:
3. Methods of Counting:
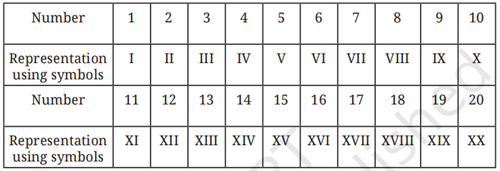
There are three methods of counting as follows:
- Representating numbers using sticks

- Representating numbers using sounds or names
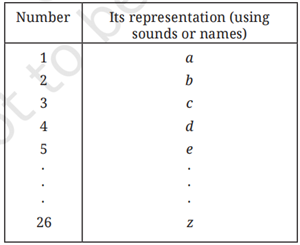
- Representating numbers using symbols
4. Some Early Number System:
- Use of Body parts:
Group of people in Papua New Guinea used and still use their body parts as the standard sequence/number system.

- Tally marks:
One of the oldest methods of number representation is by making notches—marks cut on a surface such as a bone or a wall of a cave.
These marks are also called \(\text{tally marks.}\)
In this method, a mark is made for each object that is being counted. So the final collection of marks represents the total number of objects.
- Gumulgal Number System:
Number names obtained by counting in Two's

5. Roman Numerals:
The Roman number system introduces newer symbols to represents certain bigger numbers. Let us call all these numbers that have a new basic symbol as landmark numbers. Here are some of the landmark numbers of the Roman system and their associated numerals.

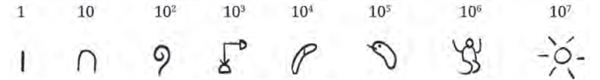
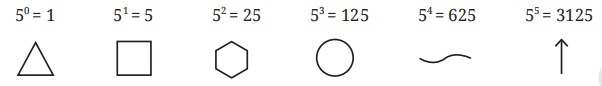

Example:
\(27\) = 10 + 10 + 5 + 5 + 1 = \(\text{XXVII}\)
\(2367\) = 1000+1000+1000+100+100+100+50+10+5+1+1 = \(\text{MMMCCCLXVII}\)
6. The Idea of base
- Egyptian Number System:
In this system, we see the use of landmark numbers to group and represent a given number. However, what makes this system special is its sequence of landmark numbers.
Each landmark number is 10 times the previous one. Since 1 is the first landmark number, they are all powers of 10. The following are the symbols given to these numbers —
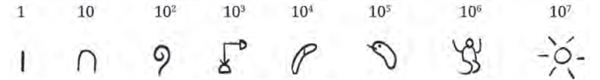
Example:
Represent \(324\) in Egyptian numerals.
Solution:
\(324 = 100+100+100+20+4\)
Thus we get, \(324\) \(=\) 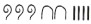
- Variation on Egyptian number system and notation of base:
We get a new number system where each landmark number is 5 times the previous one. Since 1 is the first landmark number, they are all powers of 5.
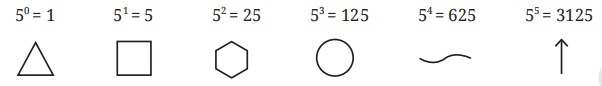
Example:
Represent \(143\) in this new number system
Solution:
\(143=125+5+5+5+1+1+1\)
\(143\) = 
Number systems having landmark numbers in which the
(a) first landmark number is 1, and
(b) every next landmark number is obtained by multiplying the current landmark number by some fixed number \(n\) is said to be \(\text{base-n}\) number system.
The Egyptian number system is a base - 10 system, and the number system that we created is a base - 5 system. A base - 10 number system is also called a \(\text{decimal number system}\)