Advantage of Base - n system:
There are two advantages in Base -n system
i) Addition of base -n system
ii) Multiplication of base -n system
Examples:
Question 1:
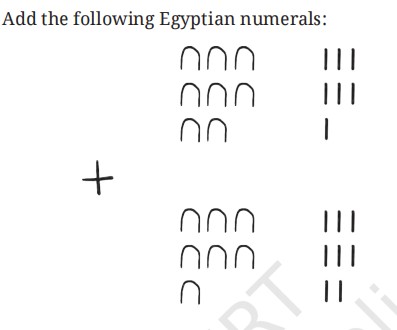
Solution:
Table value of Egyptian number system:
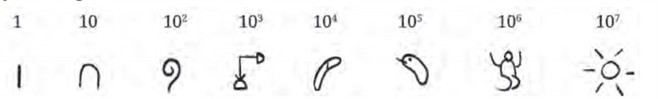
Regrouping the number of  and
and  we get,
we get,
\(15\)  and \(15\)
and \(15\) 
From the above table we get,
From the table we get,
\(10\) 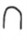 \(=\)
\(=\) 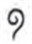
\(10\)  \(=\)
\(=\) 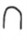
Thus we get,
\(15\) 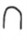 \(= (10 \)
\(= (10 \)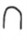 \(+\) \(5\)
\(+\) \(5\) 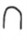
\(=\)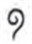
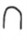
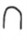
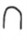
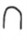
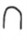 ------ (1)
------ (1)
\(= (10 + 5 ) \times 10\)
\( = (10 \times 10\) + (5 \times 10)\)
\(15\)  \(= (10 \)
\(= (10 \) \(+\) \(5\)
\(+\) \(5\) 
\(=\) 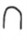




 ------ (2)
------ (2)
Thus the sum of (1) and (2)
\(=\) 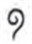
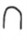
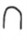
Question 2:
Find the product of the following:
Solution:
From the table we get,
\(=10^{2}\)
\(=\)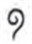
Place Value Representation:
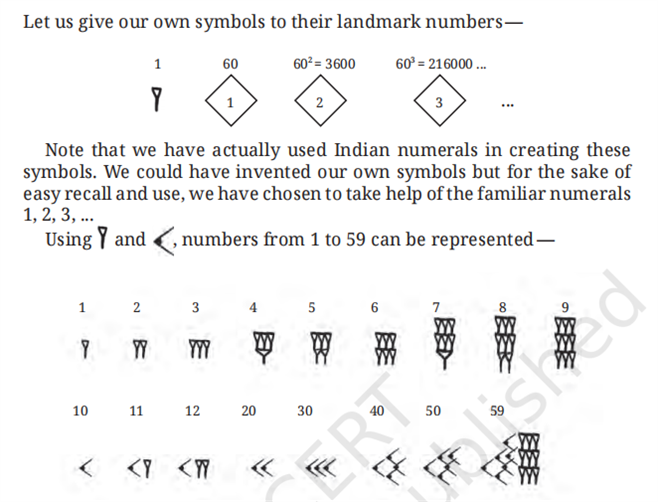
The Mesopotamian Number System
It is a \(\text{base - 60 system}\). It is also called as \(\text{sexagesimal system}\).
It is influenced by \(\text{Babylonian number system}\)
Example:
\(\text{1 hour = 60 minutes}\)
\(\text{1 minute = 60 seconds}\)
Symbols:
Example:
\( 640 = (10) \times 60 + 40\)
\(=\) \(10 \times\)  \(+ 4 \times\)
\(+ 4 \times\) 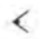
 \(+ 4 \times\)
\(+ 4 \times\) 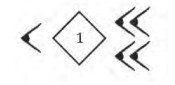
Mayan Number System

Chinese Number System:

The Hindu Number System:
