A parallelogram whose each angle is a right angle is called a rectangle.
Now we are going to define a rectangle \(ABCD\) as aquadrilateral is a parallelogram whose each interior angle is \(90^\circ\).
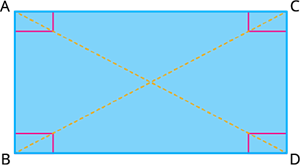
Thus, if \(ABCD\) is a rectangle then \(AB=BC=CD=AD\) and \(AB||CD\) and \(BD||AC\).
Important!
A rectangle has all the properties osf a paralleolgram with interior.
In a rectangle, the the following properties are true:
- The opposite sides are parallel and equal in length.
- The interior angles of the rectangle is \(90^\circ\).
- The diagonals are equal in measure and bisect each other.
- The adjacent angles are supplementary.
A rectangle is called a square whose adjacent sides are equal.
Now we are going to define a rectangle \(ABCD\) as aquadrilateral is a rectangle whose sides are in the same measure.

Thus, if \(ABCD\) is a rectangle then \(AB=BC=CD=AD\) and \(AB||CD\) and \(BD||AC\).
Important!
Rhombus is a special case of kite. Note that the sides of a rhombus are all of the same length; this is not the case with the kite. A rectangle has all properties of a paralelogram.
In a square, the following properties are true:
- The opposite sides are parallel.
- All the four sides are in equal measure.
- The interior angles of the square is \(90^\circ\).
- The diagonals are equal in measure and perpendicular bisector of each other.
- The adjacent angles are supplementary.
There are some properties which are always true for any parallelogram.
Let's see those properties with explanation.
In a parallelogram, the following properties are true:
- the opposite sides are equal in length.
- the opposite angles are equal in measure.
- the adjacent angles are supplementary.
- the diagonals bisect each other.
Proof:
Let's prove (1) and (2).
Let \(ABCD\) be a parallelogram.
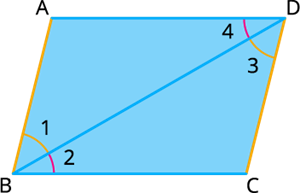
Draw a diagonal \(BD\) and denote the interior angles as \(∠1, ∠2, ∠3\) and \(∠4\).
Since \(ABCD\) is a parallelogram, \(AD\) is parallel to \(BC\) and \(AB\) is parallel to \(CD\).
Consider the parallel lines \(AD\) and \(BC\) and take the diagonal \(BD\) as transversal.
Here \(∠2 = ∠4\) by alternate interior angle property [Alternate interior angles are equal in measure].
Now consider parallel lines \(AB\) and \(CD\) and take the diagonal \(BD\) as transversal.
Here \(∠1 = ∠3\) by alternate interior angle property [Alternate interior angles are equal in measure].
So we have \(∠1 + ∠2 = ∠3+∠4\). That is, \(∠B = ∠D\).
Consider the triangles \(DAB\) and \(BCD\) with the common side \((BD = BD)\).
Now we have \(∠2 = ∠4\), \(∠1 = ∠3\) and the common side \((BD = BD)\).
By \(ASA\) criterion of congruence, \(DAB\) \(BCD\).
That is, they are congruent triangles.
Therefore, \(AD = BC, AC = CD\) and \(∠A= ∠C\).
Hence, in parallelogram \(ABCD\), we have \(AD = BC, AC = CD, ∠A = ∠C\) and \(∠B = ∠D\).
This proves (1) and (2).
From (2), it is obvious that \(∠A = ∠C\) and \(∠B = ∠D\).
Let's prove (3).
Let the measure of angles are\(∠A = ∠C = x\) and \(∠B = ∠D = y\).
We have the property that sum of all interior angles of a quadrilateral is \(360°\).
That is, \(∠A + ∠B +∠C + ∠D = 360°\).
Substituting the taken values in the above equation.
\(x + y + x + y = 360°\)
\(2x +2y = 360°\)
\(2(x + y) = 360°\)
\(x + y = 180°\).
That is, we can write this as \(∠A + ∠B = 180°\), \(∠B + ∠C = 180°\), \(∠C + ∠D = 180°\) and \(∠A + ∠D = 180°\).
It proves the property (3).
Let's prove (4).
Consider a parallelogram \(ABCD\). Draw its diagonals \(AC\) and \(BD\). Let the intersection point of the diagonals be \(O\).
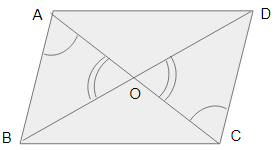
In triangle \(AOB\) and \(COD\), we have:
\(AB = CD\) as opposite sides are equal in parallelogram.
\(∠AOB = ∠COD\) [Because vertically opposite angles are equal].
Here \(AB\) is parallel to \(CD\), so \(∠OAB = ∠DCO\).
By AAS criterion of congruence, \(OAB\)\(OCD\).
This implies, \(OA = OC\) and \(OB = OD\).
As they are equal, diagonals of a parallelogram bisect each other.