A quadrilateral with one pair of parallel sides is called trapezium.
Now we are going to define a trapezium \(ABCD\) as a quadrilateral having exactly one pair of parallel sides.

Therefore, if \(ABCD\) is a trapezium in that \(AD\) is parallel to \(BC\)(\(AD||BC\)).
Here \(∠A + ∠B = 180°\) and \(∠C + ∠D = 180°\). This condition is because \(AD || BC\) and considering the line \(AB\) as transversal, the angles \(∠A\) and \(∠B\) are alternate interior and alternate exterior angles. Thus, they form a linear pair.
This implies, the angles \(∠A\) and \(∠B\) are supplementary.
Similar way, if we consider the \(CD\) as transversal, the angles \(∠C\) and \(∠D\) are supplementary.
Important!
Terms used in trapezium:
- The pair of parallel sides are called the bases while the non-parallel sides are called the legs of the trapezoid.
- The line segment connecting the midpoints of the non-parallel sides of a trapezoid is called the mid-segment.
- If we draw a line segment, between the two non-parallel sides, from the mid-point of both sides, the trapezium will be divided into two unequal parts.
In a trapezium, the following properties are true:
- The sum of all the four angles of the trapezium is equal to \(360°\).
- A trapezium has \(4\) unequal sides.
- A trapezium has two parallel sides and two non-parallel sides.
- The diagonals of trapezium bisect each other.
- The length of the mid-segment is equal to \(\frac{1}{2}\) the sum of the parallel bases, in a trapezium.
- Sum of adjacent angles on non-parallel sides of trapezium is \(180°\).
A trapezium is isosceles trapezium, if its non-parallel sides are equal.
Thus, a quadrilateral \(ABCD\) is an isosceles trapezium, if \(AD || BC\) and \(AB = CD\).

Important!
A quadrilateral is a parallelogram if its both pairs of opposite sides are parallel.
In an isosceles trapezium, the following properties are true:
- Exactly one pair of parallel sides and one pair of congruent sides.
- Diagonals are congruent and do not bisect each other.
- Base angles are congruent, and the opposite angles are supplementary.
A parallelogram with all sides are equal is called a rhombus.
Now we are going to define a rhombus \(ABCD\) as a quadrilateral is a parallelogram with all the sides are in equal measures.
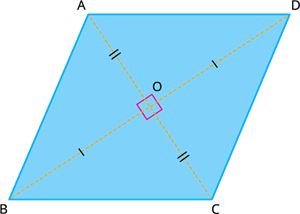
Thus, if \(ABCD\) is a rhombus then \(AB = BC = CD = AD\), \(AB || CD\) and \(BC || AD\).
Important!
Rhombus is a special case of kite. Note that the sides of a rhombus are all of the same length; this is not the case with the kite.
A rhombus has all the properties of a parallelogram and also that of a kite.
In a rhombus, the following properties are true:
- The sum of all the four angles of the rhombus is equal to \(360°\).
- The opposite sides are equal in length.
- The opposite angles are equal in measure.
- The adjacent angles are supplementary.
- The diagonals are perpendicular bisector of each other.
A quadrilateral with two pairs of equal adjacent sides and unequal opposite sides is called a kite.
Now we are going to define a kite \(ABCD\) is a quadrilateral having two pairs of equal adjacent sides and unequal opposite sides.
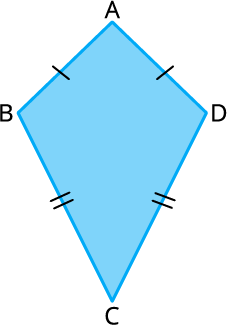
Thus, if \(ABCD\) is a kite, then \(AB = AD\) and \(BC = CD\).
In a kite, the following properties are true:
- The sum of all the four angles of the kite is equal to \(360°\).
- A kite has two pairs of equal adjacent sides.
- A kite has unequal opposite sides.
- The diagonals of kite perpendicular bisect of each other.
- One of the diagonals bisects the other diagonal.
- In the figure, \(∠B =∠D\) but \(∠A\) \(∠C\).