So far, we have discussed, the increment in the product of any two numbers \(a\) and \(b\) by \(1\).
Now, we will generalise the increase or decrease in the product \(ab\), if both \(a\) and \(b\) are increased or decreased by two different numbers say \(m\) and \(n\).
In the product \(ab\), the first number \(a\) is increased by a number \(m\) and the second number \(b\) is increased by a number \(n\).
The above statement is visualised as follows:
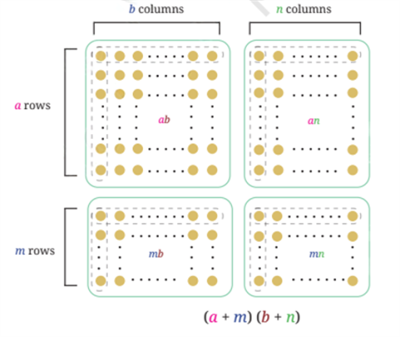
Let us find the increase in product for \((a + m)(b +n)\) using the distributive property as follows:
Expanding the product using distributive property, we have.
\((a + m)(b + n) = (a + m)b + (a + m)n)\)
\(=\) \(ab + mb + an + mn\)
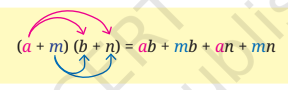
Observe that the product \(ab\) is increased by \(mb + an + mn\).
Identity 1: \((a + m)(b + n) = ab + mb + an + mn\)
Example:
Consider the product of \(a = 21\) and \(b = 19\).
Let us find the change in product if \(21\) is increased by \(2\) and \(19\) is increased by \(3\).
\((21 + 2)(19 + 3) = (21 \times 19) + (2 \times 19) + (21 \times 3) + (2 \times 3)\)
\(=\) \(21 \times 19\) \(+\) \(38 + 63 + 6\)
\(=\) \(399\) + \(\fbox{107}\)
The product is increased by \(107\).
Using the identity (1), we will solve the following cases.
- For the product \(ab\), consider \(m = u\) and \(n = -v\).
In other words, the first number \(a\) is increased by a number \(u\) and the second number \(b\) is decreased by a number \(v\).
Let us find the product of \((a + u)(b - v)\).
Expanding the product using distributive property, we have.
\((a + u)(b - v) = (a + u)b - (a + u)v\)
\(=\) \(ab + ub - av - uv\)
Thus, \((a + u)(b - v) = ab + ub - av - uv\)
- For the product \(ab\), consider \(m = -u\) and \(n = v\).
In other words, the first number \(a\) is decreased by a number \(u\) and the second number \(b\) is increased by a number \(v\).
Let us find the product of \((a - u)(b + v)\).
Expanding the product using distributive property, we have.
\((a - u)(b + v) = (a - u)b + (a - u)v\)
\(=\) \(ab - ub + av - uv\)
Thus, \((a - u)(b + v) = ab - ub + av - uv\)
- For the product \(ab\), consider \(m = -u\) and \(n = -v\).
In other words, the first number \(a\) is decreased by a number \(u\) and the second number \(b\) is decreased by \(v\).
Let us find the product of \((a - u)(b - v)\).
Expanding the product using distributive property, we have.
\((a - u)(b - v) = (a - u)b - (a - u)v\)
\(=\) \(ab - ub - av + uv\)
Thus, \((a - u)(b - v) = ab - ub - av + uv\)
Let us recall the identities we have learnt so far.
- \((a + m)(b + n) = ab + mb + an + mn\)
- \((a + u)(b - v) = ab + ub - av - uv\)
- \((a - u)(b + v) = ab - ub + av - uv\)
- \((a - u)(b - v) = ab - ub - av + uv\)
Important!
The increment in product does not always imply that the product will always increase. The product may increase or decrease based on the values of \(a\) and \(b\), depending on the type of integer choosen.
The way of generalising any algebraic expression is a method to derive an identity.
Mathematical statements that express the equality of two algebraic expression are called identities.