Consider any \(2\) by \(2\) square of numbers in a calendar, as shown in the figure.
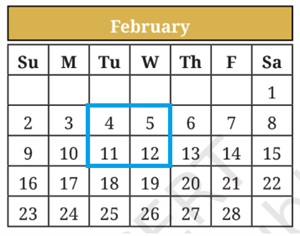
Find products of numbers lying along each diagonal — \(4 × 12 = 48\), \(5 × 11 = 55\). Do this for the other \(2\) by \(2\) squares. What do you observe about the diagonal products? Explain why this happens.
Interpretation:
Let us consider the following \(2×2\) block:

The \(2×2\) block of numbers on a calendar can be algebraically expressed as:
For any \(2×2\) block of numbers on a calendar, the product of the numbers along a diagonal exceeds the product along the other diagonal by exactly by .
This always holds true because the numbers in adjacent rows on a calendar difference by \(7\), which is due to the .
This always holds true because the numbers in adjacent rows on a calendar difference by \(7\), which is due to the .