In mathematics, diagrams and figures often permit multiple interpretations of the same region or shape. This means that a single problem can be solved through multiple valid methods. Such an approach helps us derive a relation between geometric shapes and algebraic expressions.
Solving geometric problems algebraically enables us to understand algebraic identities rather than just memorizing them. If an expression is visualized as an area or a combination of shapes, the algebra becomes more easier and intuitive.
What does "multiple methods" mean?
The concept of "multiple methods" involves the ability to interpret one diagram in two or more ways, yet arrive at the same area or value using different strategies.For example, when considering a diagram, we might think of the solution in more than one way:
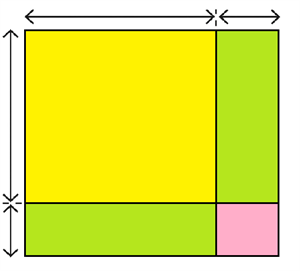
Method 1:
Calculate the required area by taking into consideration the total area of a big square by adding or subtracting its parts.
Calculate the required area by taking into consideration the total area of a big square by adding or subtracting its parts.
Method 2:
Find the area by directly recognizing the shape of the region and calculating it as a single geometric figure.
Find the area by directly recognizing the shape of the region and calculating it as a single geometric figure.
Both approaches must give the same answer, because they represent the same region.
What does this lead to?
Equating the expressions we obtained using the two methods, we naturally come up with well-known algebraic identities like:\((a+b)^2\) \(=\) \(a^2+2ab+b^2\)
\((a−b)^2 = a^2 −2ab + b^2\)
These identities become much easier to understand when they are viewed visually.
Important!
- A single geometric figure can be interpreted in more than one way, and each method produces the same result.
- This approach helps us derive and understand algebraic expressions and identities geometrically.