General expression for the square of difference of two numbers \((a-b)^{2}\):
Using the distributive property of multiplication, we expand the expression \((a-b)^{2}\) as follows:
\((a-b)^{2}\) \(=\) \((a-b)(a-b)\)
\(=\) \((a-b)a - (a-b)b\)
\(=\) \(a^{2} - ba - (ab - b^{2})\)
\(=\) \(a^{2} - ab - ab + b^{2}\) [By commutatvity \(ba = ab\)]
\(=\) \(a^{2} - 2ab + b^{2}\)
Therfore, \((a-b)^{2}\) \(=\) \(a^{2} - 2ab + b^{2}\).
Identity: \((a-b)^{2}\) \(=\) \(a^{2} - 2ab + b^{2}\)
Geometrical proof of identity:
Consider a square of area \(a^2\) whose side is \(a\).
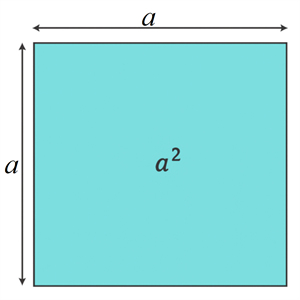
We need to find the area of the smaller square of length \((a-b)\).
For this, we need to reduce the length of the bigger square by a factor \(b\) on all its sides.
This is geometrically represented as follows:
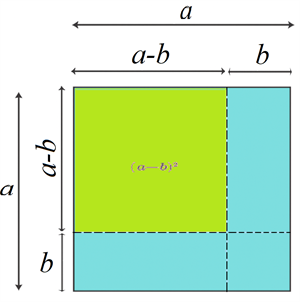
Now, let us compute the area \((a-b)^2\) as follows:
\((a-b)^2\) \(=\) \(a^2\) [Area of the bigger square] \(-\) \(2 \times ab\) [Twice the area of rectangular strips] \(+\) \(b^2\) [Area of the smallest square].
Here \(b^2\) is added back as the overlapping rectangles subtracts it twice.
Thus, \((a-b)^2\) \(=\) \(a^2 - 2ab + b^2\).
Hence, proved.
Example:
Look for the following cases where we used the identities.
1. Expand \((2x-4)^2\) using the identity.
The above expression is in \((a-b)^2\) form.
We have the identity, \((a-b)^2\) \(=\) \(a^2-2ab+b^2\).
Substitute \(a = 2x\) and \(b = 4\) in the formula.
\((2x-4)^2\) \(=\) \((2x)^2-2(2x)(4)+4^2\)
\(=\) \(4x^2-2\times 8x+16\)
\(=\) \(4x^2-16x+16\)
2. Evaluate \(98^2\) using identity.
\(98^2\) \(=\) \((100-2)^2\)
The above expression is in \((a-b)^2\) form.
We have the identity, \((a-b)^2\) \(=\) \(a^2-2ab+b^2\).
Substitute \(a = 100\) and \(b = 2\) in the formula.
\((100-2)^2\) \(=\) \(100^2-2(100)(2)+2^2\)
\(= 10000-400+4\)
\(= 9604\)