General expression for the square of sum of two numbers \((a+b)^{2}\):
Using the distributive property of multiplication, we expand the expression \((a+b)^{2}\) as follows:
\((a+b)^{2}\) \(=\) \((a+b)(a+b)\)
\(=\) \((a+b)a + (a+b)b\)
\(=\) \(a^{2} + ba + ab + b^{2}\)
\(=\) \(a^{2} + ab + ab + b^{2}\) [By commutatvity \(ba = ab\)]
\(=\) \(a^{2} + 2ab + b^{2}\)
Therfore, \((a+b)^{2}\) \(=\) \(=\) \(a^{2} + 2ab + b^{2}\).
Identity: \((a+b)^{2}\) \(=\) \(a^{2} + 2ab + b^{2}\)
Geometrical proof of identity:
Let us construct a square of four regions. The two square shaped regions with the dimensions of \(a × a\) and \(b × b\). And, the remaining two rectangle shaped regions with dimensions \(a × b\).
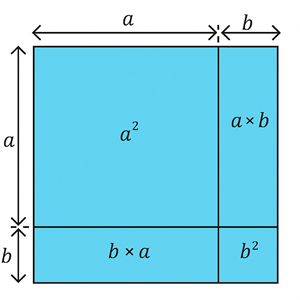
From the above figure, we get:
\(\text{Total area of the bigger square}\) \(=\) \(\text{Sum of the areas of the two small squares}\) \(+\) \(\text{Sum of the areas of the two rectangles}\)
That is, \((a + b)^2 = a^{2} + b^{2} + ba + ab\)
Since, \(ba=ab\); \((a + b)^2\) \(=\) \(a^{2} + ab + ab + b^{2}\).
Therefore, \((a + b)^2\) \(=\) \(a^{2} + 2ab+ b^{2}\).
\(\text{Total area of the bigger square}\) \(=\) \(\text{Sum of the areas of the two small squares}\) \(+\) \(\text{Sum of the areas of the two rectangles}\)
That is, \((a + b)^2 = a^{2} + b^{2} + ba + ab\)
Since, \(ba=ab\); \((a + b)^2\) \(=\) \(a^{2} + ab + ab + b^{2}\).
Therefore, \((a + b)^2\) \(=\) \(a^{2} + 2ab+ b^{2}\).
Example:
Look for the following cases where we used the identities.
1. Expand \((x+4)^2\) using the identity.
The above expression is in \((a+b)^2\) form.
We have the identity, \((a+b)^2\) \(=\) \(a^2+2ab+b^2\).
Substitute \(a = x\) and \(b = 4\) in the formula.
\((x+4)^2\) \(=\) \(x^2+2(x)(4)+4^2\)
\(=\) \(x^2+2\times 4x+16\)
\(=\) \(x^2+8x+16\)
2. Evaluate \(102^2\) using identity.
\(102^2\) \(=\) \((100+2)^2\)
The above expression is in \((a+b)^2\) form.
We have the identity, \((a+b)^2\) \(=\) \(a^2+2ab+b^2\).
Substitute \(a = 100\) and \(b = 2\) in the formula.
\((100+2)^2\) \(=\) \(100^2+2(100)(2)+2^2\)
\(= 10000+400+4\)
\(= 10404\)