
Demonstrate that in a cyclic quadrilateral, the internal bisectors of opposite angles \(B\) and \(D\) meet on a diameter of the circle.
Explanation:
Now, Join \(QD\) and \(QC\).
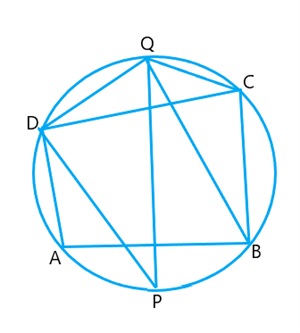
Here, \(ABCD\) is a cyclic quadrilateral.
The bisectors of opposite angles of the cyclic quadrilateral, \(∠A\) and \(∠C\), intersect the circle circumscribing at the points \(P\) and \(Q\) respectively.
Now, the opposite angles of a cyclic quadrilateral are supplementary.
That is, \(∠B + ∠D = \)\(^°\)
\(\frac{1}{2}∠B+\frac{1}{2}∠D=\frac{1}{2} \times \)\(^°\)
\(=\)\(^°\)
That is, \(∠CDP + \)\(= 90^°\)
But \(∠CBQ =\)
[]
Therefore, \(∠CDP + ∠CDQ = \)\(^°\)
\(∠\)\(= 90^°\)
Thus, \(∠PDQ\) is in semicircle. [The diameter of the circle subtends a right angle at the circumference]
Therefore, \(PQ\) is diameter of the circle.
Hence, proved.