
If two equal chords of a circle intersect each other. Verify that they are divided into equal parts at the point of intersection
Explanation:
Now, Draw \(OM⊥ AB\), \(ON⊥ CD\) and join \(OE\), where \(O\) is the centre of circle.
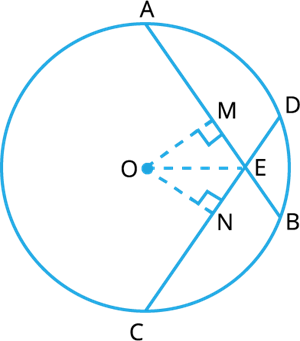
In \(△OME\) and \(△ONE\),
\(OM = \) []
\(OE = \) [common side]
Also, \(∠OME=ONE=\)\(^°\)
Therefore, \(△OME≅△ONE\) []
Now, \(EM=\) [CPCT] .....(1)
Also, \(AB = CD\).
On dividing both sides by \(2\),
\(\frac{AB}{2}=\frac{CD}{2}\)
Therefore, \(AM=\) .....(2) [Perpendicular drawn from the centre of a circle to a chord, bisects it]
Now, adding (1) and (2) we get,
\(EM + AM = EN + CN\)
Therefore, \(AE=\) .....(3)
Now, \(AB =CD \).
On subtracting \(AE\) from both the sides,
\(AB − AE = CD− AE\)
\(BE = CD − CE\) [from (3)]
That is, \(BE =\)
Hence, proved.