
In Fig., \(AB\) is a diameter of the circle, \(CD\) is a chord equal to the radius of the circle. \(AC\) and \(BD\) when extended intersect at a point \(E\). Verify that \(∠ AEB = 60^°\).
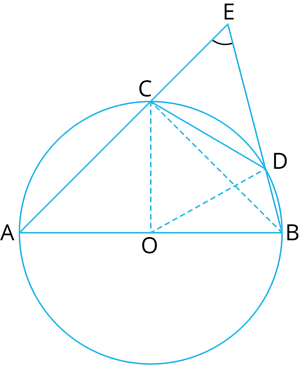
Explanation:
Join \(OC\), \(OD\) and \(BC\).
Triangle \(ODC\) is equilateral.
Therefore, \(∠ COD = \)\(^°\)
We know that, The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Therefore, \(∠ CBD = \frac{1}{2} ∠\)
This gives \(∠ CBD = \)\(^°\)
Again, \(∠ ACB = \)\(^°\) []
Since \(AE\) is a straight line, \(ACB\) and \(BCE\) forms a linear pair of angles.
\(ACB + BCE = \)\(^\circ\)
So, \(∠ BCE = 180^° – ∠ ACB = 90^°\)
In \(\bigtriangleup CEB\), \(\angle CEB + \angle BCE + \angle CBE =180^\circ\)
\(∠ CEB =180^\circ - (90^\circ + 30^\circ)\) \(=60^\circ\).
That is, \(∠ CEB = 60\)\(^°\)
Therefore, \(\angle AEB = 60^\circ\)\(^\circ\) [\(\angle CEB = \angle AEB\)].