
If in a cyclic quadrilateral both its diagonals are diameters of the circumcircle. Show that the quadrilateral is a rectangle.
Explanation:
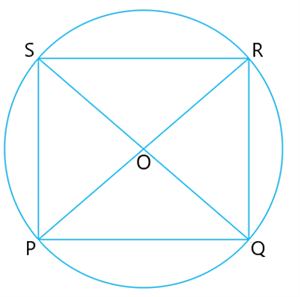
Given \(PR\) and \(QS\) are the diameters of the circle.
We know that, 'An angle inscribed in a semi-circle is a .'
Therefore, \(\angle QPS = \angle QRS = \angle PQR = \angle PSR = \)\(^\circ\) -------(1)
Now consider the triangles \(\bigtriangleup PQR\) and \(\bigtriangleup QPS\)
\(PR=\) []
\(PQ=\) []
\(\angle PQR = \angle \) [Each equal to \(90^\circ\)]
Then \(\bigtriangleup PQR \cong \bigtriangleup QPS \) [by ].
This implies, \(PS = QR\). [By C.P.CT]
similalry, \(PQ=SR\).
Therefore \(PQ = QR = RS = SP\) --------(2)
Therefore, from (1) and (2), opposite sides are equal and each angle is \(90^\circ\). Then the shape formed is a rectangle.
\(PQRS\) is a rectangle.