
Given a parallelogram
\(ABCD\), a circle passing through
\(
A\) and
\(B\) meets sides
\(AD\) and
\(
BC\) at
\(P\) and
\(
Q\). Show that points
\(M\),\(N\),\(C\), and
\(D\) are concyclic.
Given: \(ABCD\) is a parallelogram.
Let a circle whose centre is \(O\) passes through \(A\) and \(B\) such that it intersects \(AD\) at \(M\) and \(BC\) at \(N\).
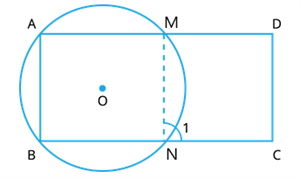
Points \(M, N, C\) and \(D\) are concyclic.
Now, Join point \(M\) to \(N\).
Thus, \(MN\) line segment is constructed.
As, \(∠1=∠\) [Exterior angle property of cyclic quadrilateral]
But \(∠A=∠\) []
Therefore, \(∠1=∠C\) .....(1)
But \(∠C+∠D=\)\(^°\) []
\(∠1+∠D=\)\(^°\) [from (1)]
Therefore, the quadrilateral \(NCDM\) is cyclic.
So, the points \(M, N, C\) and \(D\) are concyclic.
Hence, proved.