
Triangles \(WYX\) and \(WZX\) are right-angled at \(Y\)and \(Z\) respectively, and are drawn on the same hypotenuse \(WX\) but on opposite sides. Demonstrate that the angles \(∠XWY\) and \(∠XZY\) are equal.
Proof:
Now, Join \(YZ\).
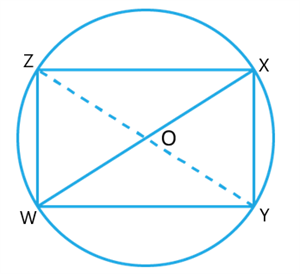
Since, \(△WYX\) and \(△WZX\) are right angled triangles.
Therefore, \(∠Y + ∠Z = \)\(^° +\) \(^°\)
\(∠Y + ∠Z =\) \(^°\)
Thus, \(WXYZ\) is a cyclic quadrilateral as sum of of a cyclic quadrilateral is \(^°\).
Also, \(∠XWY\) and \(∠XZY\) lie in the same segment and angles in the same segment of a circle are .
Therefore, \(∠XWY = ∠XZY\).
Hence, proved.