
Prove that the figure obtained by the intersection points of the internal angle bisectors of a quadrilateral is a cyclic quadrilateral.
Proof:
In Fig, \(WXYZ\) is a quadrilateral in which the angle bisectors \(WH, XF, YF\) and \(ZH\) of internal angles \(W, X, Y\) and \(Z\) respectively form a quadrilateral \(EFGH\).
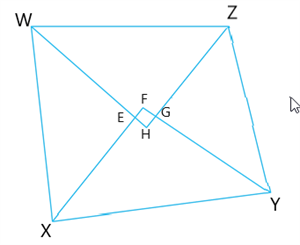
Now, \(∠ FEH = ∠\) []
In \(\bigtriangleup WEX\), \(∠ FEH = 180^°– ∠ EWX – ∠ EXW\) []
\(= 180^° –\frac{1}{2} (∠ \) \(+ ∠ \))
[Since \(WH\) and \(XF\) are the angle bisectors of \(W\) and \(X\) respectively]
Similarly, \(∠ FGH = ∠ \)
In \(\bigtriangleup YGZ\), \(= 180^° – ∠ GYZ – ∠ GZY\) []
\(= 180^° –\frac{1}{2} (∠ \) \(+ ∠ )\)
Therefore, \(∠ FEH + ∠ FGH = 180^° –\frac{1}{2} (∠ W + ∠X ) + 180^° –\frac{1}{2} (∠ Y + ∠Z )\)
\(= 360^° –\frac{1}{2} (∠ W+ ∠ X +∠ Y +∠ Z)\)
\(= 360^° –\frac{1}{2} \times\) \(^°\)
\(= 360^° – 180^° = \)\(^°\)
Since, sum of one pair of opposite angles is \(180^\circ\).
Therefore, \(EFGH\) is cyclic quadrilateral.