
Given a circle and two equal chords, \(PQ\) and \(PR\). Show that the angle bisector of \(\angle QPR\) is the line of symmetry for the angle and the arc, which must contain the circle's center.
Explanation:
Now, Join \(QR\).
Draw bisector \(PD\) of \(∠QPR\)
Therefore, \(∠QPD=∠RPD\)
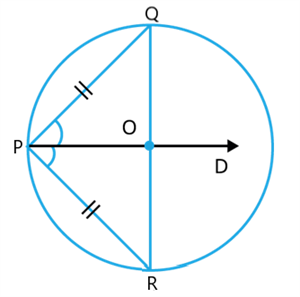
In \(△QPO\) and \(△RPO\),
\(PQ = \) (given)
\(∠QPO=∠\) (by construction)
\(PO =\) []
Therefore, \(△QPO≅△RPO\) []
That is, \(QO = RO\) [by ] and
\(∠QOP=∠ROP\) [by ]
Also, \(QO = RO\) and \(∠QOP=∠ROP=\)\(^°\)
Thus, \(PO\) is the perpendicular bisector of the chord \(QR\).
Therefore, the bisector of \(∠QPR\)
That is., \(PD\) passes through the centre \(O\).
Hence proved.