
In a circle, two chords of equal length cut each other at a point inside the circle. Verify that the line drawn from the centre to the point of intersection bisects the angle between the chords.
Explanation:
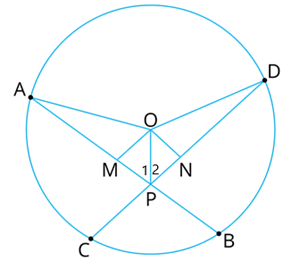
Draw \(OM\) perpendicular \(AB\) & \(ON\) perpendicular \(CD\).
In \(∆OMP\) & \(∆ONP\),
\(\angle M= \angle N=\)\(^°\)
\(OP=\) []
\(OM=\)
[ ]
Therefore, \(∆OMP≅∆ONP\) ———-[R.H.S]
Hence, \(∠1=∠2\) ———–[]