
Prove that a trapezium having equal non-parallel sides is a cyclic.
Proof:
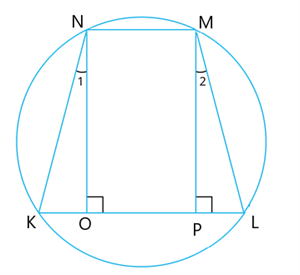
Draw \(NO\) perpendicular \(KL\) and \(MP\) perpendicular \(KL\).
In \(∆NOK\) and \(∆MPL\),
\(∠O=∠P= \)\(^°\)
\(KN=\) [given]
\(NO=\) [distance between parallel lines is same]
Therefore, \(∆NOK≅∆MPL\) [By ]
\(∠K=∠\) [by ] ----(1)
\(∠1=∠2\) [by c.p.c.t]
In trapezium \(KLMN\), \(\angle MNK +\angle NKL = \)\(^\circ\)
[In a trapezium, angles on the non-parallel sides are supplement to each other]
\(\angle MNK + \angle KLM= \)\(^\circ\) [from (1), \(\angle K = \angle L\)] ----------(2)
From (2), we can see that sum of opposite angles are supplementary.
Hence, \(KLMN\) is a cyclic quadrilateral.