1. In the Fig. , if \(∠1 = ∠3\), \(∠2 = ∠4\) and \(∠3 = ∠4\), write the relation between \(∠1\) and \(∠2\), using an Euclid’s axiom.

2. In Fig. we have : \(AC = XD\), \(C\) is the mid-point of \(AB\) and \(D\) is the mid-point of \(XY\). Using an Euclid’s axiom, show that \(AB = XY\).
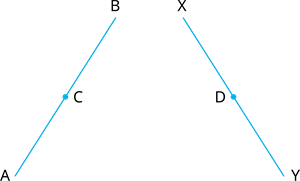
Proof:
\(AB =\) (\(C\) is the mid-point of \(AB\))
\(XY =\) (\(D\) is the mid-point of \(XY\))
Also, \(AC = XD\) (Given)
Therefore, \(AB = XY\), because things which are double of the same things are equal to one another.
Answer variants:
\(∠1 = ∠2\)
\(\angle 1+\angle 2=90^{\circ}\)
\(\frac{XD}{2}\)
\(2AC\)
\(\angle 1+\angle 2=180^{\circ}\)
\(2XD\)
\(\frac{AC}{2}\)