Solve the given question using appropriate Euclid’s axiom : In the Figure, we have \(X\) and \(Y\) are the mid-points of \(AC\) and \(BC\) and \(AX = CY\). Show that \(AC = BC\).
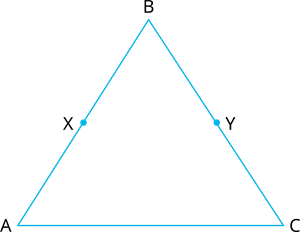
Proof:
\(X\) is mid-point of \(AC\)
Therefore, \(2AX=\) .....(1)
Also, \(Y\) is mid-point of \(BC\).
Therefore, \(2BY=\) .....(2)
Also, AX = CY (given) .....(3)
According to Euclid axiom, 'things which are double of same things are equal to one another'.
\(AX=CY\) [From (3)]
\(AC=BC\) [From (1) and (2)]
Hence, verified.