1. In the Fig. we have \(∠ABC = ∠ACB\), \(∠3 = ∠4\). Show that \(∠1 = ∠2\).
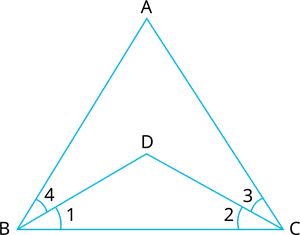
Proof:
\(∠ABC=∠ACB\) .....(1)
\(∠4=∠3\) .....(2)
By Euclid axiom \(3\)
We get the result.
\(∠1=∠2\).
2. In the Fig., we have \(AC = DC\), \(CB = CE\). Show that \(AB = DE\).
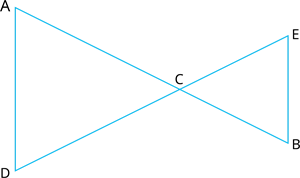
Proof:
\(AC = DC\) ---(1)
\(CB = CE\) ----)2)
By Euclid axiom \(2\),
Answer variants:
if equal are subtracted from equal, the remainders are equal.
if equal are added to equals, the wholes are equal.