Solve the given question using appropriate Euclid’s axiom : In the Figure, we have \(M\) and \(N\) are the mid-points of \(PR\) and \(QR\) and \(PM = RN\). Show that \(PR = QR\).
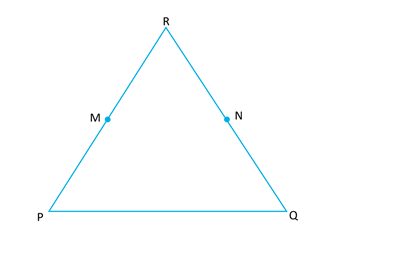
Proof:
\(M\) is mid-point of \(PR\)
Therefore, \(2AX=\) .....(1)
Also, \(N\) is mid-point of \(QR\).
Therefore, \(2QN=\) .....(2)
Also, \(PM = RN\) (given) .....(3)
According to Euclid axiom, 'things which are double of same things are equal to one another'.
\(PM = RN\) [From (3)]
\(PR =QR\) [From (1) and (2)]
Hence, verified.