1. In the Fig. we have \(∠PQR= ∠PRQ\), \(∠3 = ∠4\). Show that \(∠1 = ∠2\).
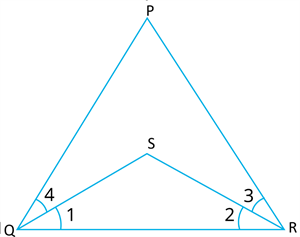
Proof:
\(∠PQR= ∠PRQ\) .....(1)
\(∠4=∠3\) .....(2)
By Euclid axiom \(3\)
We get the result.
\(∠1=∠2\).
2. In the Fig., we have \(PR = SR\), \(RQ = RT\). Show that \(PQ = ST\).
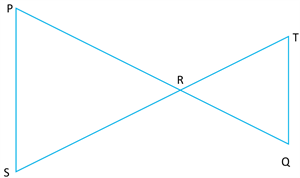
Proof:
\(PR = SR\) ---(1)
\(RQ = RT\) ----)2)
By Euclid axiom \(2\),
Answer variants:
if equal are added to equals, the wholes are equal.
if equal are subtracted from equal, the remainders are equal.