1. Derive the given question using appropriate Euclid’s axiom : Look at the Figure.
Show that length \( AG>\) sum of lengths of \(AB + BC + CD\).
Answer:
\(AB + BC + CD\) =
\( AB+BC+CD+DE+EF+FG\) =
+ \(DE+EF+FG\) =
Therefore, length of \(AG>\) Sum of length of \(AB + BC + CD\).
2. Workout the given question using appropriate Euclid’s axiom : In the Figure, we have \( AB= BC\), \( BX= BY\). Show that \( AX= CY\).
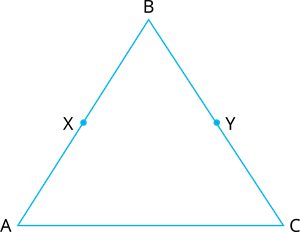
Taking
\( AB= BC\) .....(1)
\(BX= BY\) .....(2)
(2) from (1), we get
\( AB− BX =\) \(−BY\)
By Euclid Third axiom: 'If are subtracted from ,the remainder are equal.'
Thus \( AX= CY\)
Hence, verified.