In the following figure, \(OD\) is the bisector of \(∠AOC\), \(OE\) is the bisector of \(∠BOC\) and \(OD ⊥ OE\). Show that the points \(A, O\) and \(B\) are collinear.
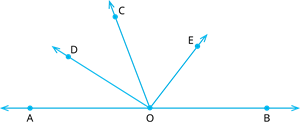
Proof:
Since, \(OD\) and \(OE\) bisect angles \(∠AOC\) and \(∠BOC\), respectively.
\(∠AOC =\) ----(1)
\(∠COB = \) ----(2)
Now, adding equation (1) and (2), we get,
\(∠AOC + ∠COB =\) \(+\)
\(∠AOC +∠COB =2\) \(+\)
\(∠AOC + ∠COB= 2\)
\(∠AOC+ ∠COB = 2 \times \) \(^°\) [Since \(OD ⊥ OE\)]
By simplifying this then we get, \(∠AOB = 180^°\)
Hence, \(∠AOC\) and \(∠COB\) are forming linear pair.
Also, \(AOB\) is a straight line.
Hence, points \(A, O\) and \(B\) are collinear.