Bisectors of angles \(B\) and \(C\) of a triangle \(ABC\) intersect each other at the point \(O\). Prove that \(∠BOC = 90^° + \frac{1}{2} ∠A\).
Proof:
Let \(ABC\) be the triangle with bisectors of angles \(B\) and \(C\) of a triangle \(ABC\) intersect each other at the point \(O\) as shown in below figure.
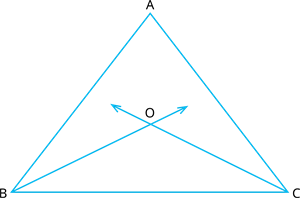
\(∠A + ∠ABC + ∠ACB =\) \(^°\) (Angle sum property of a triangle)
Therefore, \(\frac{1}{2} ∠A + \frac{1}{2} ∠ABC + \frac{1}{2} ∠ACB = \frac{1}{2} \times \)\(^° =\) \(^°\)
That is., \(\frac{1}{2} ∠A + ∠OBC + ∠OCB = \)\(^°\) (Since \(BO\) and \(CO\) are bisectors of \(∠B\) and \(∠C\)) -----(1)
But \(∠BOC + ∠OBC + ∠OCB =\)\(^°\) (Angle sum property) -------(2)
Subtracting (1) from (2), we have
\(∠BOC + ∠OBC + ∠OCB – \frac{1}{2} ∠A – ∠OBC – ∠OCB =\) \(-\)
By simplyfing this then we get the result.