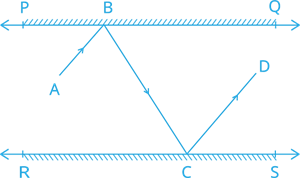
In given figure, \(PQ\) and \(RS\) are two mirrors placed parallel to each other. An incident ray \(AB\) strikes the mirror \(PQ\) at \(B\), the reflected ray moves along the path \(BC\) and strikes the mirror \(RS\) at \(C\) and again reflects back along \(CD\). Prove that \(AB || CD\).
Proof:
Draw ray \(BL ⊥ PQ\) and \(CM ⊥ RS\)
Draw ray \(BL ⊥ PQ\) and \(CM ⊥ RS\)
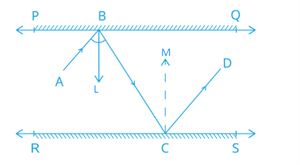
Here, \(PQ || RS\) and \(BL || CM\)
Now, \(BL || CM\) and \(BC\) is a transversal
\(∠LBC = ∠\) [ Alternate interior angles ]
Since, angle of incidence \(=\) angle of reflection
\(∠ABL = ∠LBC\) and \(∠MCB = ∠MCD\)
Therefore, \(∠ABL = ∠\)----(2)
Adding (1) and (2) and simplyfing then we get,
\(∠ABC = ∠BCD\)
That is, a pair of alternate angles are equal.
Thus, \(AB || CD\).
Hence, Proved.