A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
Proof:
Consider \(AB\) and \(CD\) to be the two parallel lines and are intersected by transversal \(GH\) at \(P\) and \(Q\).
Now, \(EP\) and \(FQ\) be the bisectors of corresponding angles \(∠APG\) and \(∠CQP\).
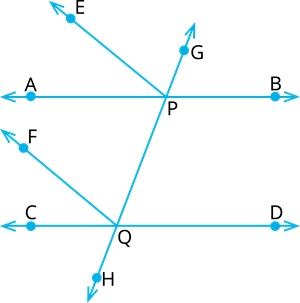
Since, \(AB∥CD\) .
\(∠APG=∠\) [Corresponding angles]
\(\frac{1}{2}∠APG=\frac{1}{2}∠\)
\(∠EPG=∠\) [Since, \(EP\) and \(FQ\) are bisectors]
As, the corresponding angle made by the lines \(EP\) and \(FQ\) and the transversal line \(GH\) are \(∠EPG\) and \(∠FQP\) and they are equal.
Hence, \(EP∥FQ\).