In Fig., \(BA || ED\) and \(BC || EF\). Show that \(∠ABC = ∠DEF\) [Hint: Produce \(DE\) to intersect \(BC\) at \(P\) (say)].
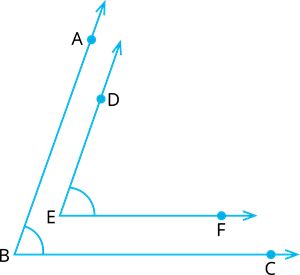
Proof:
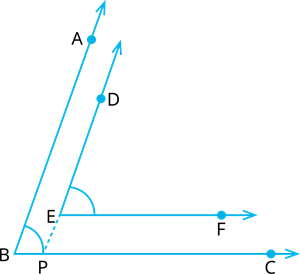
Produce \(DE\) to intersect \(BC\) at \(P\).
\(EF II BC\) and \(DP\) is the transversal.
\(∠DEF=∠\) [Corresponding angles] ----(1)
Now, \(AB∥DP\) and \(BC\) is the transversal.
\(∠DPC=∠\) [Corresponding angles] -----(2)
From (1) and (2), We get the result.