In Fig.,\(m\) and \(n\) are two plane mirrors perpendicular to each other. Show that incident ray \(CA\) is parallel to reflected ray \(BD\).
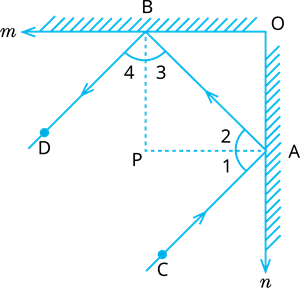
Proof:
Let normals at \(A\) and \(B\) meet at \(P\).
As mirrors are perpendicular to each other
Therefore, \(BP ||\) and \(AP ||\).
So, \(BP ⊥ PA\),
That is, \(∠ BPA = 90^°\)
Therefore, \(∠ 3 + ∠ 2 =\)\(^°\) (Angle sum property) ------(1)
Also, \(∠1 = ∠2\) and \(∠4 = ∠3\) (Angle of incidence \(=\) Angle of reflection)
Therefore, \(∠1 + ∠4 =\)\(^°\)-----(2)
Adding (1) and (2),
we have \(∠1 + ∠2 + ∠3 + ∠4 =\)\(^°\)
That is, \(∠CAB + ∠DBA =\)\(^°\)
Hence, \(CA || BD\)