In Fig., \(OP, OQ, OR\) and \(OS\) are four rays. Prove that \(∠ POQ + ∠ QOR + ∠ SOR + ∠ POS = 360^°\)
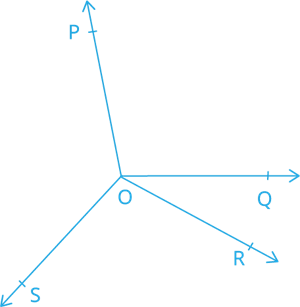
Proof:
Let us produce ray \(OQ\) backwards to a point \(T\) so that \(TOQ\) is a line.
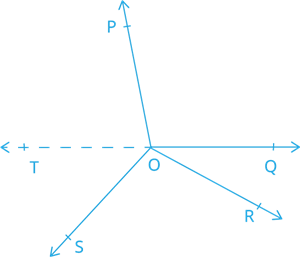
Now, ray \(OP\) stands on line \(TOQ\).
Therefore, \(∠ TOP + ∠ POQ =\)\(^°\)---- (1) (Linear pair axiom)
Similarly, ray \(OS\) stands on line \(TOQ\).
Therefore, \(∠ TOS + ∠ SOQ =\)\(^°\) ---- (2)
But \(∠ SOQ = ∠ SOR + ∠ QOR\)
So, (2) becomes \(∠ TOS + ∠ SOR + ∠ QOR =\)\(^°\) ----(3)
Now, adding (1) and (3), you get \(∠ TOP + ∠ POQ + ∠ TOS + ∠ SOR + ∠ QOR = 360^°\) ------- (4)
But \(∠ TOP + ∠ TOS = ∠ POS\)
Therefore, (4) becomes \(∠ POQ + ∠ QOR + ∠ SOR + ∠ POS = 360^°\)
Hence Proved.