In the figure, \(∠Q > ∠R\), \(PA\) is the bisector of \(∠QPR\) and \(PM ⊥ QR\). Prove that \(∠APM=\frac{1}{2}(∠Q−∠R)\).
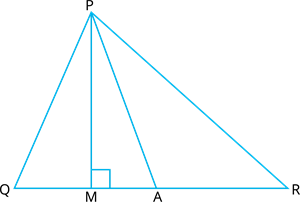
Proof:
\(PA\) is bisector of \(∠QPR\) .
Therefore, \(∠QPA=∠APR\) ----- (1)
In \(△ PQM\), by angle sum property of triangles,
\(∠PQM+∠PMQ+∠QPM=\)\(^°\)
\(∠PQM+\)\(^°+∠QPM=\)\(^°\)
\(∠PQM=\)\(^°−∠QPM\)
\(∠Q=\)\(^°−∠QPM\) --------(2)
Again, in \(△ PMR\), by angle sum property of triangles,
\(∠PMR+∠PRM+∠RPM=\)\(^°\)
\(^°+∠PRM+∠RPM=\)\(^°\)
\(∠PRM=\)\(^°−∠RPM\)
\(∠R=\)\(^°−∠RPM\) -------.(3)
Subtracting (3) from (2), and simplifying then we get,
\(=2∠APM\) (From (1))
\(∠APM=\frac{1}{2} [∠Q−∠R]\)