In the following figure, if \(x + y = w + z\), then prove that \(AOB\) is a line.
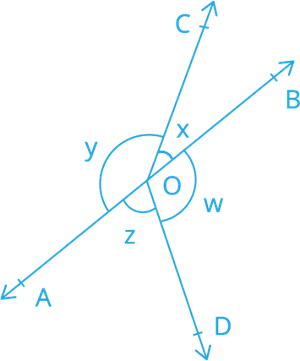
Proof:
We know that , sum of all angles made along a point is \(^°\)
From the given figure, \(∠AOC + ∠BOC + ∠BOD + ∠AOD =\)\(^°\)
\(y + x + w + z =\)\(^°\)
From (1), \((x + y) + (x + y) =\)\(^°\)
\(x +\)\(y =\)\(^°\)
\((x + y) =\)\(^°\)
\(x + y=\)\(^°\)
From this statement it is proved that \(AOB\) is a straight line because the sum of angles made on the line is \(^°\).
So, \(AOB\) is a straight line.
Hence Proved.